题目内容
【题目】在矩形![]() 的
的![]() 边上取一点
边上取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处.
处.
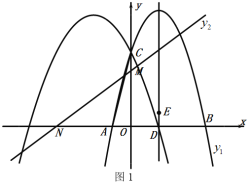
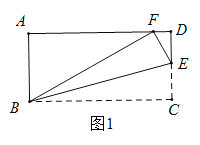
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
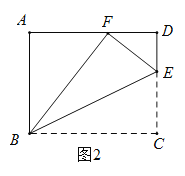
(2)如图2,当![]() ,且
,且![]() 时,求
时,求![]() 的长;
的长;
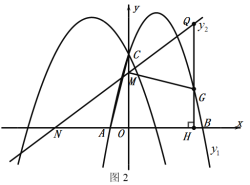
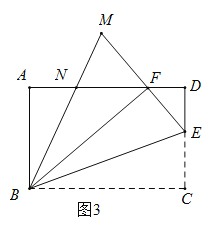
(3)如图3,延长![]() ,与
,与![]() 的角平分线交于点
的角平分线交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 出的值.
出的值.
【答案】(1)15°;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据矩形的性质和直角三角形的性质,先得到![]() ,再由折叠的性质可得到
,再由折叠的性质可得到![]() ;
;
(2)由三等角证得![]() ,从而得
,从而得![]() ,
,![]() ,再由勾股定理求出DE,则
,再由勾股定理求出DE,则![]() ;
;
(3)过点![]() 作
作![]() 于点
于点![]() ,可证得
,可证得![]() .再根据相似三角形的性质得出对应边成比例及角平分线的性质即可得解.
.再根据相似三角形的性质得出对应边成比例及角平分线的性质即可得解.
(1)∵矩形![]() ,
,
∴![]() ,
,![]()
由折叠的性质可知BF=BC=2AB,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
(2)由题意可得![]() ,
,
![]() ,
,
![]()
∴![]()
∴![]()
∴![]() ,
,
∴![]()
∴![]() ,
,
由勾股定理得![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)过点![]() 作
作![]() 于点
于点![]() .
.
∴![]()
又∵![]()
∴![]() .
.
∴![]() .
.
∵![]() ,即
,即![]()
∴![]() ,
,
又∵BM平分![]() ,
,![]() ,
,
∴NG=AN,
∴![]() ,
,
∴
整理得:![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目