Question

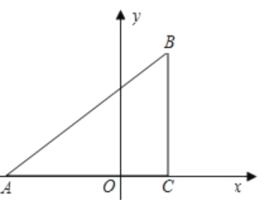
【题目】已知：如图，在平面直角坐标系中，是直角三角形，，点的坐标分别为，

(1)求过点的直线的函数表达式

(2)在轴上找一点，连接，使得与相似（不包括全等），并求点的坐标；

(3)在⑵的条件下，如分别是和上的动点，连接，设，问是否存在这样的使得与相似，如果存在，请求出的值；如果不存在，请说明理由．

Answer 1

【答案】(1) y=x+; (2) D（，0）；(3)

【解析】

（1）设过点A(-3,0)，B(1,3)的直线的函数表达式为y=kx+b，

由 0=k×(-3)+b ，

3=k+b

解得k=,b=，

∴直线AB的函数表达式为y=x+.

(2)如图，过点B作BD⊥AB，交x轴于点D，

在Rt△ABC和Rt△ADB中，

∵∠BAC=∠DAB，

∴Rt△ABC∽Rt△ADB，

∴D点为所求，

又tan∠ADB=tan∠ABC=，

∴CD=BC÷tan∠ADB=3÷=，

∴OD=OC+CD=，∴D（，0）；

(3)这样的m存在．

在Rt△ABC中，由勾股定理得AB=5，

如图，

当PQ∥BD时，△APQ∽△ABD，则，

解得m=，

如图，

当PQ⊥AD时，△APQ∽△ADB，

则

解得m=．