题目内容
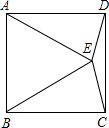正方形ABCD内一点，如果△ABE为等边三角形，那么∠DCE为
- A.30°
- B.25°
- C.15°
- D.20°
C
分析：由四边形ABCD是正方形可以得出AB=BC=CD=AD，∠ABC=∠BCD=∠CDA=∠DAB=90°，由△ABE为等边三角形可以得出AB=BE=AE，∠BAE=∠AEB=∠ABE=60°，可以求出BE=BC，∠CBE=30°，进而可以求出∠BCE=75°，故可以求出∠DCE的度数．
解答：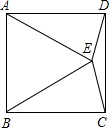
解：∵四边形ABCD是正方形，
∴AB=BC=CD=AD，∠ABC=∠BCD=∠CDA=∠DAB=90°．
∵△ABE为等边三角形，
∴AB=BE=AE，∠BAE=∠AEB=∠ABE=60°．
∴BE=BC，∠EBC=30°，
∴∠BEC=∠BCE=75°，
∴∠DCE=90°-75°=15°．
故选C．
点评：本题考查了等边三角形的性质，正方形的性质及等腰三角形的性质的运用，在解答的过程中利用边相等构建等腰三角形是解答的关键．
分析：由四边形ABCD是正方形可以得出AB=BC=CD=AD，∠ABC=∠BCD=∠CDA=∠DAB=90°，由△ABE为等边三角形可以得出AB=BE=AE，∠BAE=∠AEB=∠ABE=60°，可以求出BE=BC，∠CBE=30°，进而可以求出∠BCE=75°，故可以求出∠DCE的度数．
解答：
解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠ABC=∠BCD=∠CDA=∠DAB=90°．
∵△ABE为等边三角形，
∴AB=BE=AE，∠BAE=∠AEB=∠ABE=60°．
∴BE=BC，∠EBC=30°，
∴∠BEC=∠BCE=75°，
∴∠DCE=90°-75°=15°．
故选C．
点评：本题考查了等边三角形的性质，正方形的性质及等腰三角形的性质的运用，在解答的过程中利用边相等构建等腰三角形是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
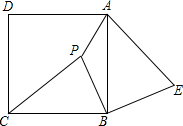已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE=∠CBP，BE=BP．
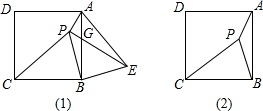如图（1），P是正方形ABCD内一点，将△PBC绕点B按顺时针方向旋转后与△EBA重合．
如图，P是正方形ABCD内一点，将△ABP绕B顺时针旋转90°到△CBP′位置，若BP=a，则PP′=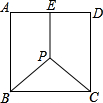
如图，正方形ABCD内一点P，PE⊥AD于E，若PB=PC=PE=5，则正方形的边长为