题目内容
5. 如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠1=∠2,∠BPA=∠CQA,试判断△APQ的形状,并说明理由.
如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠1=∠2,∠BPA=∠CQA,试判断△APQ的形状,并说明理由.
分析 先证△ABP≌△ACD得AP=AD,再证∠PAD=60°,从而得出△APD是等边三角形.
解答 解:△APQ是等边三角形.
理由如下:∵AB=AC,∠1=∠2,∠BPA=∠CQA,
∴△ABP≌△ACQ,
∴∠BAP=∠CAQ,AP=AQ,
∴∠PAQ=∠CAQ+∠PAC=∠BAP+∠PAC=∠BAC=60°,
∴△APQ是等边三角形.
点评 本题考查了等边三角形的判定与性质及全等三角形的判定方法,注意条件与问题之间的联系.

练习册系列答案
相关题目
15.绝对值不大于3的整数的个数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
20.下列长度的三条线段能组成三角形的是( )
| A. | 1,2,4 | B. | 4,9,6 | C. | 5,5,11 | D. | 3,5,8 |
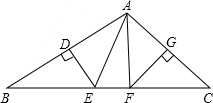 △ABC中,DE,FG分别垂直平分边AB,AC,垂足分别为点D,G.
△ABC中,DE,FG分别垂直平分边AB,AC,垂足分别为点D,G.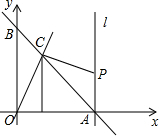 如图,直线y=-x+6与坐标轴交于A、B两点,与直线y=2x交于C点,直线是过A点且垂直x轴的直线,点P是直线l上的一动点.
如图,直线y=-x+6与坐标轴交于A、B两点,与直线y=2x交于C点,直线是过A点且垂直x轴的直线,点P是直线l上的一动点.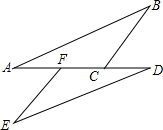 如图,在△ABC和△DEF中,AF=DC,∠A=∠D.当添加条件BC=EF时,可依据“SAS”证明△ABC≌△DEF;当添加条件∠ACB=∠DFE时,可依据”ASA”证明△ABC≌△DEF,当添加条件∠B=∠E时,可依据”AAS”证明△ABC≌△DEF.
如图,在△ABC和△DEF中,AF=DC,∠A=∠D.当添加条件BC=EF时,可依据“SAS”证明△ABC≌△DEF;当添加条件∠ACB=∠DFE时,可依据”ASA”证明△ABC≌△DEF,当添加条件∠B=∠E时,可依据”AAS”证明△ABC≌△DEF.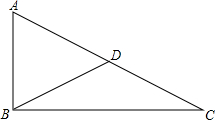 已知在△ABC中,∠A=3∠C,∠ADB=45°,D为AC的中点,求证:∠ABC=90°.
已知在△ABC中,∠A=3∠C,∠ADB=45°,D为AC的中点,求证:∠ABC=90°.