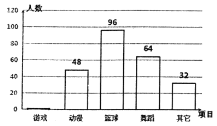
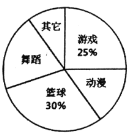
��Ŀ����
����Ŀ��ƽ��ֱ������ϵ�У�����y��![]() ��x��0����ͼ��G������A��4��1������ֱ��y��
��x��0����ͼ��G������A��4��1������ֱ��y��![]() x+b��ͼ���ڵ�B����y�ύ�ڵ�C�����кᡢ�����궼�������ĵ�������㣮��ͼ��G�ڵ�A��B֮��IJ������߶�OA��OC��BCΧ�ɵ��������߽磩ΪW����W��ǡ��4�����㣬��Ϻ���ͼ��b��ȡֵ��Χ�ǣ�������
x+b��ͼ���ڵ�B����y�ύ�ڵ�C�����кᡢ�����궼�������ĵ�������㣮��ͼ��G�ڵ�A��B֮��IJ������߶�OA��OC��BCΧ�ɵ��������߽磩ΪW����W��ǡ��4�����㣬��Ϻ���ͼ��b��ȡֵ��Χ�ǣ�������
A.��![]() ��b��1��
��b��1��![]() ��b��
��b��![]() B.��
B.��![]() ��b��1��
��b��1��![]() ��b��
��b��![]()
C.��![]() ��b����1��
��b����1��![]() ��b��
��b��![]() D.��
D.��![]() ��b����1��
��b����1��![]() ��b��
��b��![]()
���𰸡�D
��������
����ֱ��BC��y=![]() x+b��OAƽ�У������������ֱ��l��OA���·����Ϸ�����ͼ��������W��ǡ��4�����㣬ȷ��b��ȡֵ��Χ��
x+b��OAƽ�У������������ֱ��l��OA���·����Ϸ�����ͼ��������W��ǡ��4�����㣬ȷ��b��ȡֵ��Χ��
�⣺��ͼ1��ֱ��l��OA���·�ʱ��

��ֱ��l��y��![]() x+b����0����1��ʱ��b����1���Ҿ�����4��0���㣬����W�����������㣬
x+b����0����1��ʱ��b����1���Ҿ�����4��0���㣬����W�����������㣬
��ֱ��l��y��![]() x+b����1����1��ʱ��b����
x+b����1����1��ʱ��b����![]() ���Ҿ�����5��0��������W�����������㣬
���Ҿ�����5��0��������W�����������㣬
������W��ǡ��4�����㣬b��ȡֵ��Χ�ǩ�![]() ��b����1��
��b����1��
��ͼ2��ֱ��l��OA���Ϸ�ʱ��

�ߵ㣨2��2���ں���y��![]() ��x��0����ͼ��G��
��x��0����ͼ��G��
��ֱ��l��y��![]() x+b����1��2��ʱ��b��
x+b����1��2��ʱ��b��![]() ��
��
��ֱ��l��y��![]() x+b����1��3��ʱ��b��
x+b����1��3��ʱ��b��![]() ��
��
������W��ǡ��4�����㣬b��ȡֵ��Χ��![]() ��b��
��b��![]() ��
��
��������������W��ǡ��4�����㣬b��ȡֵ��Χ�ǩ�![]() ��b����1��
��b����1��![]() ��b��
��b��![]() ��
��
��ѡ��D��

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�����Ŀ��ij��ѧ���������40�����ʵ��������ij��˾����һ�Ҽ��˵꾭Ӫ���˽һ�ֳɱ�Ϊ20Ԫ/����������Ʒ�ڵ�![]() �����۵������Ϣ���±���ʾ��
�����۵������Ϣ���±���ʾ��
������ |
|
���۵��� | �� �� |
��1�������ڼ������Ʒ�����۵���Ϊ35Ԫ/����
��2����40���иü��˵�ڼ����õ����������������Ƕ��٣�
��3����ʵ�����۵�ǰ20���У���˾Ϊ�������˵���մ�ѧ���μ�ʵ�������ÿ����һ����Ʒ�ͷ����ü��˵�![]() Ԫ������ͨ���ü��˵�����ۼ�¼���֣�ǰ10���У�ÿ���ý������������ʱ��
Ԫ������ͨ���ü��˵�����ۼ�¼���֣�ǰ10���У�ÿ���ý������������ʱ��![]() ���죩�������������
���죩�������������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��