Question

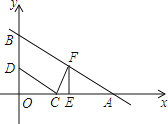
【题目】如图，已知某写字楼AB的正前方有一座信号塔DE，在高为60m的楼顶B处，测得塔尖E处的仰角为30°，从楼底A处向信号塔方向走30m到达C处，测得塔尖E处的仰角为68°，已知点D，C，A在同一水平线上，求信号塔DE的高度．（结果精确到0.1m.参考数据：sin68°≈0.9，cos68°≈0.4，tan 68°≈2.5，≈1.7）.

Answer 1

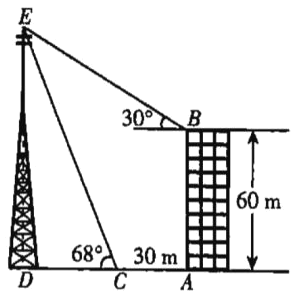
【答案】信号塔DE的高度约为101.5m．

【解析】

过点B作BG⊥DE于点G，设CD＝xm，在△CDE中，得到DE＝CD·tan 68°（m），进而得到EG＝DE－GD＝（2.5x－60）m；在△EGB中，得到BG＝EG＝1.7（2.5x－60）m，因为BG＝AD，所以1.7（2.5x－60）＝x＋30，求解即可.

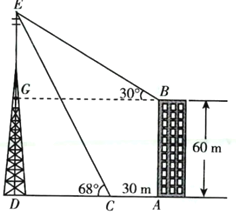
过点B作BG⊥DE于点G.

设CD＝xm，

在△CDE中，∠EDC＝90°，∠ECD＝68°，

则＝tan 68°，

∴DE＝CD·tan 68°（m）.

∵GD＝AB＝60m，

∴EG＝DE－GD＝（2.5x－60）m

在△EGB中，∠EGB＝90°，∠EBG＝30°

则＝tan 30°，

∴BG＝EG＝1.7（2.5x－60）m.

∴BG＝AD，

∴1.7（2.5x－60）＝x＋30，

解得x＝

则DE＝2.5×＝101.5（m）.

答：信号塔DE的高度约为101.5m.