Question

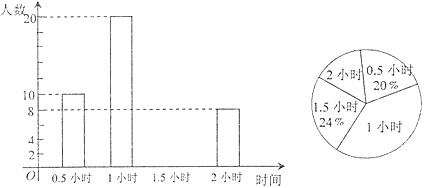
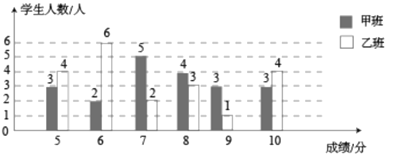
【题目】中华人民共和国第二届青年运动会(简称二青会)将于2019年8月在山西举行，太原市作为主赛区，将承担多项赛事，现正从某高校的甲、乙两班分别招募10人作为颁奖礼仪志愿者，同学们踊跃报名，甲、乙两班各报了20人，现已对他们进行了基本素质测评，满分10分.各班按测评成绩从高分到低分顺序各录用10人，对这次基本素质测评中甲、乙两班学生的成绩绘制了如图所示的统计图.

请解答下列问题：

(1)甲班的小华和乙班的小丽基本素质测评成绩都为7分，请你分别判断小华，小丽能否被录用(只写判断结果，不必写理由).

(2)请你对甲、乙两班各被录用的10名志愿者的成绩作出评价(从“众数”，“中位数”，或“平均数”中的一个方面评价即可).

(3)甲、乙两班被录用的每一位志愿者都将通过抽取卡片的方式决定去以下四个场馆中的两个场馆进行颁奖礼仪服务，四个场馆分别为：太原学院足球场，太原市沙滩排球场，山西省射击射箭训练基地，太原水上运动中心，这四个场馆分别用字母A，B，C，D的四张卡片(除字母外，其余都相同)背面朝上，洗匀放好.志愿者小玲从中随机抽取一张(不放回)，再从中随机抽取一张，请你用列表或画树状图的方法求小玲抽到的两张卡片恰好是“A”和“B”的概率.

Answer 1

【答案】(1)小华：不能被录用，小丽：能被录用；(2)见解析；(3).

【解析】

(1)根据甲班超过7分的人数，乙班超过6分的人数都正好为10人进行说明即可；

(2)求出甲、乙两班的众数，从众数角度进行说明；也可以求出中位数，从中位数角度进行说明；还可以求出两班的平均数，从平均数角度进行说明；(只要用其中一个进行说明即可)；

(3)画树状图得到所有等可能的情况数，然后找出符合条件的情况数，利用概率公式进行计算即可.

(1)甲班超过7分的人数有4+3+3=10人，因此从高到低录取，小华不能被录取；

乙班超过7分的人数有3+1+4=8人，超过6分的人数有2+3+1+4=10人，因此从高到低录取，小丽能被录用；

(2)从众数来看：甲、乙两班各被录用的10名志愿者成绩的众数分别为8分，10分，说明甲班被录用的10 名志愿者中8分最多，乙班被录用的10名志愿者中10分最多；

从中位数来看：甲、乙两班各被录用的10名志愿者成绩的中位数分别为9分，8.5分，说明甲班被录用的10名志愿者成绩的中位数大于乙班被录用的10名志愿者成绩的中位数；

从平均数来看：甲、乙两班各被录用的10名志愿者成绩的平均数分别为=8.9，=8.7，说明甲班被录用的10名志愿者成绩的平均数大于乙班被录用的10名志愿者成绩的平均数；

(从“众数”，“中位数”或“平均数”中的一方面即可)；

(3)画树状图如下：

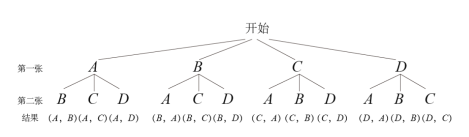
由树状图可知一共有12种可能出现的结果，且每种结果出现的可能性相同，其中抽到“A”和“B”的结果有2种.∴.