Question

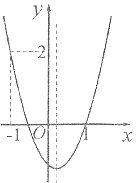
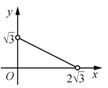
【题目】已知：二次函数(a为常数)．

(1)请写出该二次函数图象的三条性质；

(2)在同一直角坐标系中，若该二次函数的图象在的部分与一次函数的图象有两个交点，求的取值范围．

Answer 1

【答案】(1)见解析；(2)．

【解析】

(1)可从开口方向、对称轴、最值等角度来研究即可；

(2) 先由二次函数的图象与一次函数的图象有两个交点，即关于x的一元二次方程有两个不相等的实数根，由此可得，再根据二次函数的图象在的部分与一次函数的图象有两个交点，也就是说二次函数的图象与轴的部分有两个交点，画出函数的图象，结合图象，可知当时，，将x=4代入求得a的取值范围，由此即可求得答案.

(1)①图象开口向上；②图象的对称轴为直线；③当时，随的增大而增大；④当时，随的增大而减小；⑤当时，函数有最小值；

(2)∵二次函数的图象与一次函数的图象有两个交点，

∴，即，

，解得，

∵二次函数的图象在的部分与一次函数的图象有两个交点，

∴二次函数的图象与轴的部分有两个交点，

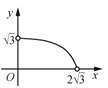
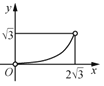
画出二次函数的图象，结合图象，

可知当时，，

∴当时，，得，

∴当二次函数的图象在的部分与一次函数的图象有两个交点时，

的取值范围为．