题目内容
1．
如图，P、Q、R是双曲线y=$\frac{k}{x}$（k＜0）上的三点，过这三点分别作y轴的垂线，垂足分别是A、B、C，连OP、OQ、QR得到△POA、△QOB、△ROC，设它们的面积分别是S1、S2、S3，则S1、S2、S3大小关系是（ ）| A． | S1＜S2＜S3 | B． | S2＜S1＜S3 | C． | S1＜S3＜S2 | D． | S1=S2=S3 |
分析 直接根据反比例函数比例系数k的几何意义求解．
解答 解：因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S1=S2=S3=$\frac{1}{2}$|k|．
故选D．
点评 本题考查了反比例函数比例系数k的几何意义：在反比例函数y=$\frac{k}{x}$图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
练习册系列答案
相关题目
11．矩形有而菱形不具有的性质是（ ）
| A． | 对角线互相垂直 | B． | 对角线相等 | C． | 对角线互相平分 | D． | 四条边都相等 |
12．下列各数中互为相反数的是（ ）
| A． | -$\frac{1}{2}$与0.2 | B． | $\frac{1}{3}$与-0.33 | C． | -2.25与2$\frac{1}{4}$ | D． | 5与-（-5） |
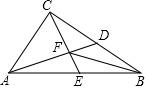如图，在Rt△ABC中，∠ACB=90°，AD、CE分别是BC、AB边上的中线，且满足AD⊥CE，垂足为F，联结BF．
如图，∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，依此类推，若OA1=1，则△A2016B2016A2017的边长为（ ）