题目内容
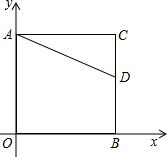
某生活小区临街的一面有块如图所示的梯形空地，物业部门打算把这块空地美化一下，以供观赏．初步打算沿对角线AC，BD修两条小路，把梯形ABCD分成四块，种上相同种类的花．四块地的面积分别为S1，S2，S3，S4，一位物业工人很快看出S3，S4两种需要花的棵数大致相等．（1）你知道他是根据什么判断的吗？（说明S3与S4之间关系的理由？）
（2）请你用学过的知识探究S1，S2，S3三者之间的关系？
考点：面积及等积变换
专题：常规题型
分析：（1）先判断出S△ADC=S△DCB，继而分别利用两者表示出S3、S4，继而可判断出S3与S4之间的关系．
（2）根据高相同的两三角形的面积之比等于底边之比可得出S1：S3，S2：S4，结合（1）的结论可得出S1，S2，S3三者之间的关系．
（2）根据高相同的两三角形的面积之比等于底边之比可得出S1：S3，S2：S4，结合（1）的结论可得出S1，S2，S3三者之间的关系．
解答：解：（1）S△ADC=S△DCB（等底等高）
所以S3=S4
（2）
→
=
→S3=
．
|
所以S3=S4
（2）
|
| S1 |
| S3 |
| S3 |
| S2 |
| S1S2 |
点评：此题考查了面积及等积变换的知识，解答本题关键是掌握等底的两三角形面积之比等于高之比，难度一般在，注意仔细观察图形．
练习册系列答案
相关题目
设M=3n+2×17n，其中n为正整数，则下列结论正确的是（ ）
| A、有且只有一个n，使得M为完全平方数 |
| B、存在多于一个的有限个n，使得M为完全平方数 |
| C、存在无数个n，使得M为完全平方数 |
| D、不存在n，使得M为完全平方数 |
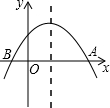如图，已知抛物线y=x2+bx+c与坐标轴交于A、B两点，则一元二次方程x2+bx+c=0的根的情况是（ ）| A、没有实数根 |
| B、有两个相等的实数根 |
| C、有两个不相等的实数根 |
| D、可能有实数根，也可能没有实数根 |
如图，正方形AOBC的B点在x轴正半轴上，A在y轴正半轴上，边长为
如图，一根木棒（AB）长2a，斜靠在与地面（OM）垂直的墙壁（ON）上，与地面的倾斜角（∠ABO）为60°．若木棒A端沿直线ON下滑，且B端沿直线OM向右滑行（NO⊥OM），于是木棒的中点P也随之运动，已知A端下滑到A′时，