题目内容
 G为△ABC的重心,△ABC的三边长满足AB>BC>CA,记△GAB,△GBC,△GCA的面积分别为S1、S2、S3,则有
G为△ABC的重心,△ABC的三边长满足AB>BC>CA,记△GAB,△GBC,△GCA的面积分别为S1、S2、S3,则有
- A.S1>S2>S3
- B.S1=S2=S3
- C.S1<S2<S3
- D.S1S2S3的大小关系不确定
B
分析:根据三角形的重心是三角形三条中线的交点,可以延长CG交AB于点D,则可求得S2=S3,同理可证明S1=S2,故S1、S2、S3面积关系可求.
解答: 解:如图,延长CG交AB于点D
解:如图,延长CG交AB于点D
则△ACD的面积=△BCD的面积,△AGD的面积=△BGD的面积
∴S2=S3
同理可证明S1=S2
∴S1=S2=S3
故选B.
点评:考查了重心的概念.根据三角形的面积公式,可知三角形的重心是三角形三条中线的交点,可以把三角形分割成面积相等的两部分.
分析:根据三角形的重心是三角形三条中线的交点,可以延长CG交AB于点D,则可求得S2=S3,同理可证明S1=S2,故S1、S2、S3面积关系可求.
解答:
 解:如图,延长CG交AB于点D
解:如图,延长CG交AB于点D则△ACD的面积=△BCD的面积,△AGD的面积=△BGD的面积
∴S2=S3
同理可证明S1=S2
∴S1=S2=S3
故选B.
点评:考查了重心的概念.根据三角形的面积公式,可知三角形的重心是三角形三条中线的交点,可以把三角形分割成面积相等的两部分.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
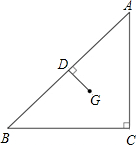 如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )
如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )| A、7 | ||
B、14
| ||
C、
| ||
D、
|
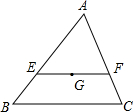 如图,G为△ABC的重心,若EF过点G且EF∥BC,交AB、AC于E、F,则
如图,G为△ABC的重心,若EF过点G且EF∥BC,交AB、AC于E、F,则 2、如图所示,△ABC,D,E,F三点将BC四等分,AG:AC=1:3,H为AB的中点,下列哪一个点为△ABC的重心( )
2、如图所示,△ABC,D,E,F三点将BC四等分,AG:AC=1:3,H为AB的中点,下列哪一个点为△ABC的重心( ) 14、如图,E为△ABC的重心,ED=3,则AD=
14、如图,E为△ABC的重心,ED=3,则AD= (2013•闸北区二模)已知:如图,△ABC中,点D、E、F分别在边BC、CA、AB上,
(2013•闸北区二模)已知:如图,△ABC中,点D、E、F分别在边BC、CA、AB上,