题目内容
【题目】如图所示,再平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),![]() ,点C的坐标为(0,3).
,点C的坐标为(0,3).
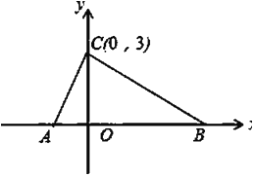
(1)求a,b的值;
(2)求![]() ;
;
(3)若点M在坐标轴上,且![]() =
=![]()
![]() ,直接写出M的坐标;
,直接写出M的坐标;
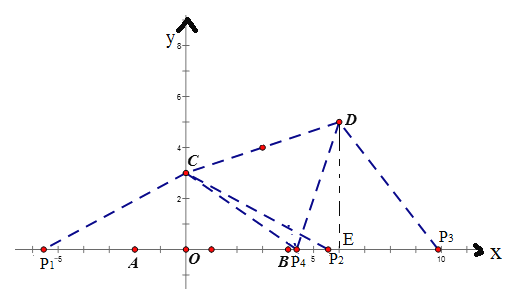
(4)点D的坐标为(6,5),动点P在x轴上,当△CDP试等腰三角形,请直接写出所有符合条件的点P的坐标.
【答案】(1)a=-2,b=4;(2)9;(3)(0,0)或(-4,0);(4)P1(-![]() ,0),P2(
,0),P2(![]() ,0),P3(
,0),P3(![]() ,0),P4(
,0),P4(![]() ,0).
,0).
【解析】
(1)根据绝对值和算术平方根的非负性,求出a、b的值,求得A、B的坐标;
(2)根据三角形的面积公式求解;
(3)当M在![]() 轴上时,设点M的坐标为(x,0),根据AM的距离和三角形的面积S△ACM=
轴上时,设点M的坐标为(x,0),根据AM的距离和三角形的面积S△ACM=![]() S△ABC可求出AM的值,从而得到M的坐标;当M在
S△ABC可求出AM的值,从而得到M的坐标;当M在![]() 轴上时,设点M的坐标为
轴上时,设点M的坐标为![]() ,则
,则![]() 以
以![]() 为底,以
为底,以![]() 为高,根据S△ACM=
为高,根据S△ACM=![]() S△ABC可求出
S△ABC可求出![]() 的值,即可得到M的坐标.
的值,即可得到M的坐标.
(4)通过作图,可得: 当以∠C为顶角时,对应P1,P2;当以∠D为顶角时,对应P3;当以CD为底时,对应P4;根据勾股定理求解.
解:(1)∵|a+2|+![]() =0,∴a+2=0,b-4=0.
=0,∴a+2=0,b-4=0.
∴a=-2,b=4.
(2)由(1)得;点A(-2,0),点B(4,0).
又∵点C(0,3),
∴AB=|-2-4|=6,CO=3.
∴S三角形ABC=![]() AB·CO=
AB·CO=![]() ×6×3=9.
×6×3=9.
(3) 当M在![]() 轴上时,设点M的坐标为(x,0),
轴上时,设点M的坐标为(x,0),
则AM=|x-(-2)|=|x+2|.
又∵S△ACM=![]() S△ABC,
S△ABC,
∴![]() AM·OC=
AM·OC=![]() ×9,
×9,
∴![]() |x+2|×3=3.
|x+2|×3=3.
∴|x+2|=2.即x+2=±2,
解得x=0或-4,
所以点M的坐标为(0,0)或(-4,0).
当M在![]() 轴上时,设点M的坐标为
轴上时,设点M的坐标为![]() ,
,
则![]() ,
,
∵S△ACM=![]() S△ABC
S△ABC
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() .
.
所以点M的坐标为![]() 或
或![]() .
.
综上,点M的坐标为![]() ,
,![]() 或
或![]() .
.
(4)如图,点P的位置有四种情况:
当以∠C为顶角时,对应P1,P2;
当以∠D为顶角时,对应P3;
当以CD为底时,对应P4;
由已知可得:CD=![]()
所以OP1=OP2=![]() , EP3=
, EP3=![]()
所以P1(-![]() ,0),P2(
,0),P2(![]() ,0),P3(
,0),P3(![]() ,0)
,0)
设P4(x,0),则根据等腰三角形性质和勾股定理可得:
![]()
解得
![]()
所以P4(![]() ,0)
,0)
综合上述:P1(-![]() ,0),P2(
,0),P2(![]() ,0),P3(
,0),P3(![]() ,0),P4(
,0),P4(![]() ,0)
,0)