题目内容
已知x为实数,且x2+| 1 |
| x2 |
| 1 |
| x3 |
分析:根据x2+
=3,可求出
+x的值,把x3+
变形为含有x2+
与
+x的形式即可.
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x3 |
| 1 |
| x2 |
| 1 |
| x |
解答:解:∵x2+
=(x+
)2-2=3,
故
+x=±
,
又∵x3+
=(x+
)(x2-1+
)=±
×2
=±2
.
故答案为:±2
.
| 1 |
| x2 |
| 1 |
| x |
故
| 1 |
| x |
| 5 |
又∵x3+
| 1 |
| x3 |
| 1 |
| x |
| 1 |
| x2 |
| 5 |
=±2
| 5 |
故答案为:±2
| 5 |
点评:本题考查了完全平方公式,属于基础题,关键是利用完全平方公式进行变形求解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 =3,则x3+
=3,则x3+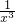 的值是________.
的值是________.