题目内容
8.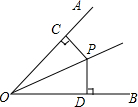 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )| A. | PC=PD | B. | ∠CPO=∠DOP | C. | ∠CPO=∠DPO | D. | OC=OD |
分析 只要证明△OPC≌△OPD,可得PC=PD,OC=OD,∠CPO=∠DPO,由此即可判断.
解答 解: 在△OPC和△OPD中,
在△OPC和△OPD中,
$\left\{\begin{array}{l}{∠POC=∠POD}\\{∠PCO=∠PDO=90°}\\{OP=OP}\end{array}\right.$,
∴△OPC≌△OPD,
∴PC=PD,OC=OD,∠CPO=∠DPO,
∴A、C、D正确,
故选B.
点评 本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形的全等条件,属于中考基础题.

练习册系列答案
相关题目
1.为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
(1)若某用户六月份用水量为18t,求其应缴纳的水费;
(2)记该用户六月份用水量为xt,缴纳水费y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40t,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
| 月用水量/t | 单价/(元/t) |
| 不大于10t部分 | 1.5 |
| 大于10t且不大于mt部分20≤m≤50 | 2 |
| 大于mt部分 | 3 |
(2)记该用户六月份用水量为xt,缴纳水费y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40t,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )
x | … | ﹣2 | 0 | 1 | 2 | … |
y | … | 7 | ﹣1 | ﹣2 | ﹣1 | … |
A. 抛物线开口向下 B. 抛物线的对称轴是y轴
C. 当x<2时,y随x的增大而减小 D. 抛物线与y轴交于负半轴
 甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图是甲乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.
甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图是甲乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.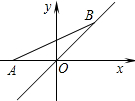 如图,点A的坐标为(-2$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB长最短时点B的坐标为(-$\sqrt{2}$,-$\sqrt{2}$).
如图,点A的坐标为(-2$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB长最短时点B的坐标为(-$\sqrt{2}$,-$\sqrt{2}$).