题目内容
13. 如图,正方形ABCD中,对角线AC、BD相交于O点,M、N分别在OA、OB上,且OM=ON.
如图,正方形ABCD中,对角线AC、BD相交于O点,M、N分别在OA、OB上,且OM=ON.(1)求证:
①BM=CN;
②CN⊥BM;
(2)若M、N分别在OA、OB的延长线上,则(1)中的两个结论仍成立吗?请说明理由.
分析 (1)①延长CN交BM于P,由四边形ABCD是正方形,得到OC=OB,∠COB=∠BOA=90°,于是推出△CON≌△BOM,结论可得,②根据全等三角形的性质即可得到结论;
(2)成立,延长MB交CN于P,通过证明△CON≌△BOM,得到BM=CN,∠ONC=∠OMB根据等角的余角相等即可得到结论.
解答 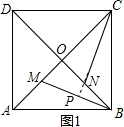 (1)①证明;如图1,延长CN交BM于P,
(1)①证明;如图1,延长CN交BM于P,
∵四边形ABCD是正方形,
∴OC=OB,∠COB=∠BOA=90°,
在△CON与△BOM中,$\left\{\begin{array}{l}{OC=OB}\\{∠COB=∠BOA}\\{ON=OM}\end{array}\right.$,
∴△CON≌△BOM,
∴BM=CN,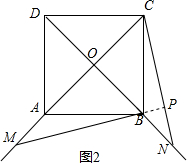
②∵△CON≌△BOM,
∴∠OCN=∠OBM,
∵∠OBM+∠OMB=90°,
∴∠OCP+∠OMB=90°,
∴∠CPM=90°,
∴CN⊥BM;
(2)成立,
证明;如图2,延长MB交CN于P,
∵四边形ABCD是正方形,
∴OC=OB,∠COB=∠BOA=90°,
在△CON与△BOM中,$\left\{\begin{array}{l}{OC=OB}\\{∠COB=∠BOA}\\{ON=OM}\end{array}\right.$,
∴△CON≌△BOM,
∴BM=CN,∠ONC=∠OMB
∵∠CNO+∠OCN=90°,
∴∠OMP+∠OCN=90°,
∴∠CPM=90°,
∴CN⊥BM.
点评 本题考查了全等三角形的判定和性质,正方形的性质,正确的作出图形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.具备下列条件的两个三角形可以判定它们全等的是( )
| A. | 一边和这边上的高对应相等 | |
| B. | 两边和第三边上的高对应相等 | |
| C. | 两边和其中一边的对角对应相等 | |
| D. | 两个直角三角形中的一条直角边、斜边对应相等 |
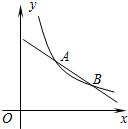 如图,反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的图象交于点A(m,m+1)、B(m+3,m-1).
如图,反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的图象交于点A(m,m+1)、B(m+3,m-1).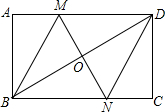 已知:如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
已知:如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.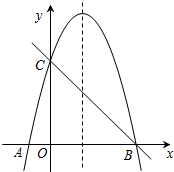 如图,抛物线y=ax2+bx-4a的对称轴为直线x=$\frac{3}{2}$,与x轴交于A,B两点,与y轴交于点C(0,4).
如图,抛物线y=ax2+bx-4a的对称轴为直线x=$\frac{3}{2}$,与x轴交于A,B两点,与y轴交于点C(0,4). 如图,电车通过A站经B站到C站,然后返回,去时在B站停车,而返回时不停,去的车速为每小时48千米.
如图,电车通过A站经B站到C站,然后返回,去时在B站停车,而返回时不停,去的车速为每小时48千米. 如图,某校数学兴趣小组利用自制的测角仪测量学校旗杆的高度,他们先在旗杆前的平地上选择一点C,用测角仪测得旗杆顶端A的仰角是50°,然后在C点和旗杆之间选择一点D(C、D、B三点在同一直线上),测出由D点看A点的仰角是62°,量得CD=3米,测角仪的高度是1.5米.
如图,某校数学兴趣小组利用自制的测角仪测量学校旗杆的高度,他们先在旗杆前的平地上选择一点C,用测角仪测得旗杆顶端A的仰角是50°,然后在C点和旗杆之间选择一点D(C、D、B三点在同一直线上),测出由D点看A点的仰角是62°,量得CD=3米,测角仪的高度是1.5米.