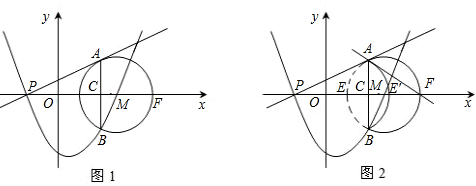题目内容
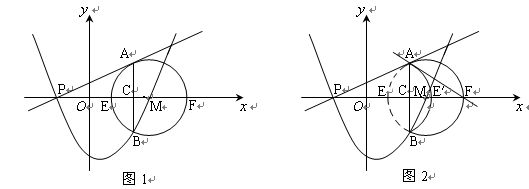
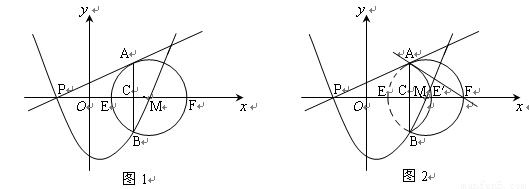
如图弧AEB与弧AFB有公共弦AB=6，D是弦AB上的一点，AD=x，点E、F分别是弧AEB与弧AFB的中点，P是EF上的中点，y=AP2-DP2，则y与x的函数关系式是
- A.
- B.
- C.
- D.
C
分析：延长PF交AB于点G，根据点E、F分别是弧AEB与弧AFB的中点可得PG⊥AB且AG=
AB，然后表示出DG，再利用勾股定理列式表示出PD2，代入等式得到y、x的函数关系式，从而得解．
解答：
解：如图，延长PF交AB于点G，
∵点E、F分别是弧AEB与弧AFB的中点，
∴PG⊥AG，AG=AB=×6=3，
∵AD=x，
∴DG=3-x，
在Rt△PDG中，PD2=PG2+DG2，
即PD2=PG2+（3-x）2，
∴y=AP2-DP2=y=AP2-PG2-（3-x）2，
在Rt△APG中，AG2=AP2-PG2=32=9，
∴y=-（3-x）2+9，
当y=0时，-（3-x）2+9=0，整理得x2-6x=0，
解得x1=0，x2=6，
纵观各选项，只有C选项图形符合．
故选C．
点评：本题考查了动点问题的函数图象，作出辅助线，构造出直角三角形求出y、x的函数关系式是解题的关键．
分析：延长PF交AB于点G，根据点E、F分别是弧AEB与弧AFB的中点可得PG⊥AB且AG=
AB，然后表示出DG，再利用勾股定理列式表示出PD2，代入等式得到y、x的函数关系式，从而得解．解答：
解：如图，延长PF交AB于点G，∵点E、F分别是弧AEB与弧AFB的中点，
∴PG⊥AG，AG=
AB=×6=3，∵AD=x，
∴DG=3-x，
在Rt△PDG中，PD2=PG2+DG2，
即PD2=PG2+（3-x）2，
∴y=AP2-DP2=y=AP2-PG2-（3-x）2，
在Rt△APG中，AG2=AP2-PG2=32=9，
∴y=-（3-x）2+9，
当y=0时，-（3-x）2+9=0，整理得x2-6x=0，
解得x1=0，x2=6，
纵观各选项，只有C选项图形符合．
故选C．
点评：本题考查了动点问题的函数图象，作出辅助线，构造出直角三角形求出y、x的函数关系式是解题的关键．
练习册系列答案
黄冈创优卷系列答案
相关题目
