题目内容
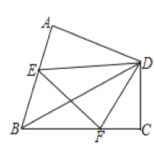
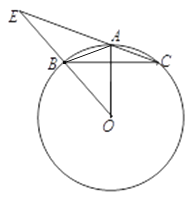
【题目】如图,△ABC内接于⊙O,AB=AC,连接并延长OB交CA延长线于点E.
(1)求证: OA平分∠BAC;
(2)若tan∠ABC=![]() ,AC=
,AC=![]() . 求⊙O的半径和线段BE的长.
. 求⊙O的半径和线段BE的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)连接OC.由AB=AC,得到弧AB=弧AC ,从而得到∠AOB=∠AOC .由等腰三角形的性质得到OA⊥BC,即可得出结论.
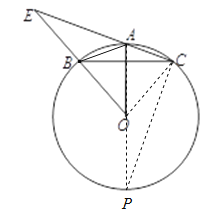
(2)延长AO交圆于P ,连接PC.由tan∠P=tan∠ABC=![]() ,得到PC,AP的长,即可得到半径.证明△EBA∽△EAO,得到
,得到PC,AP的长,即可得到半径.证明△EBA∽△EAO,得到 ![]() .设BE=
.设BE=![]() x,则AE=5x,OE=OB+BE=5+
x,则AE=5x,OE=OB+BE=5+![]() x,得到
x,得到![]() ,解方程即可得到结论.
,解方程即可得到结论.
详解:(1)连接OC.
∵AB=AC,∴弧AB=弧AC ,∴∠AOB=∠AOC .
∵OB=OC, ∴OA⊥BC.
∵AB=AC,∴OA平分∠BAC.
(2)延长AO交圆于P ,连接PC.tan∠P=tan∠ABC=![]() ,
,
∴PC=3AC=![]() ,AP=10,∴r=5.
,AP=10,∴r=5.
∵AB=AC,∴∠ABC=∠ACB.
∵∠EAB=∠ABC+∠ACB=2∠ACB=∠AOB,∠E=∠E,
∴△EBA∽△EAO,∴ ![]() .
.
设BE=![]() x,则AE=5x,OE=OB+BE=5+
x,则AE=5x,OE=OB+BE=5+![]() x,
x,
∴![]() ,解得:x=
,解得:x=![]() ,∴BE=
,∴BE=![]() x=
x=![]() .
.

练习册系列答案
相关题目
【题目】某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩![]() 及其方差S2如表所示:
及其方差S2如表所示:
甲 | 乙 | 丙 | 丁 | |
(环) | 8.4 | 8.6 | 8.6 | 7.6 |
S2 | 0.74 | 0.56 | 0.94 | 1.92 |
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁