题目内容
 如图,正方体的棱长为6cm,P为棱FG上的一点,PG=2cm,经过棱BC画AP的最短连线,交棱BC于Q点,经过棱BF也画AP的最短连线,交棱BF于R点,求从A点到P点的最短路线有几条?
如图,正方体的棱长为6cm,P为棱FG上的一点,PG=2cm,经过棱BC画AP的最短连线,交棱BC于Q点,经过棱BF也画AP的最短连线,交棱BF于R点,求从A点到P点的最短路线有几条?考点:平面展开-最短路径问题
专题:
分析:根据题意得出,可将A点所在的平面与P点所在的平面展开成平面图形,即可确定两点之间的最短路径.
解答: 解:由题意得,经过棱EF画AP的最短连线,交棱EF于M点;
解:由题意得,经过棱EF画AP的最短连线,交棱EF于M点;
经过棱EH画AP的最短连线,交棱EH于N点;
所以从A点到P点的最短路线有四条:
A→Q→P;A→R→P;A→M→P;A→N→P.
 解:由题意得,经过棱EF画AP的最短连线,交棱EF于M点;
解:由题意得,经过棱EF画AP的最短连线,交棱EF于M点;经过棱EH画AP的最短连线,交棱EH于N点;
所以从A点到P点的最短路线有四条:
A→Q→P;A→R→P;A→M→P;A→N→P.
点评:本题考查了平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图,已知四边形ABCD中,∠ABC=120°,AD⊥BA,CD⊥BC,测得AB=30
如图,已知四边形ABCD中,∠ABC=120°,AD⊥BA,CD⊥BC,测得AB=30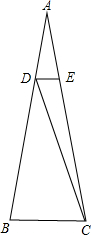 等腰△ABC中,AB=AC,∠A=20°,AD=BC,DE∥BC,求∠DCE的度数.
等腰△ABC中,AB=AC,∠A=20°,AD=BC,DE∥BC,求∠DCE的度数. 如图,有长为24m的篱笆,一面利用墙(墙长为10m)围成长方形养鸡场,设养鸡场的长BC为x m,面积为y m2.请问:当长方形的长、宽分别为多少时,养鸡场的面积最大,最大面积是多少?
如图,有长为24m的篱笆,一面利用墙(墙长为10m)围成长方形养鸡场,设养鸡场的长BC为x m,面积为y m2.请问:当长方形的长、宽分别为多少时,养鸡场的面积最大,最大面积是多少?