题目内容
如图,平行四边形ABCD中,AB=3 cm,BC=5 cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.
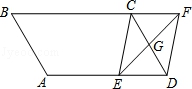
(1)证明:∵ 四边形ABCD是平行四边形,
∴ CF∥ED,∴ ∠FCG=∠EDG.
∵ G是CD的中点,∴CG=DG.
在△FCG和△EDG中,
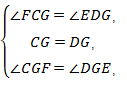
∴ △FCG≌△EDG(ASA),
∴ FG=EG.
∵ CG=DG,∴ 四边形CEDF是平行四边形;
(2)①解:当AE=3.5 cm时,平行四边形CEDF是矩形.
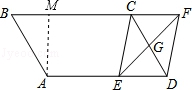 理由是:过A作AM⊥BC于M,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,
∴BM=1.5 cm.
∵ 四边形ABCD是平行四边形,
 ∴ ∠CDA=∠B=60°,DC=AB=3 cm,BC=AD=5 cm.
∴ ∠CDA=∠B=60°,DC=AB=3 cm,BC=AD=5 cm.
∵ AE=3.5 cm,∴ DE=1.5 cm =BM.
在△MBA和△EDC中,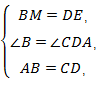
∴ △MBA≌△EDC(SAS),
∴ ∠CED=∠AMB=90°.
∵ 四边形CEDF是平行四边形,
∴ 四边形CEDF是矩形.
②当AE=2 cm时,四边形CEDF是菱形.
理由是:∵ AD=5 cm,AE=2 cm,∴ DE=3 cm.
∵ CD=3,∠CDE=60°,
∴ △CDE是等边三角形,∴ CE=DE.
∵ 四边形CEDF是平行四边形,
∴ 四边形CEDF是菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
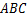 中,若三边长分别为9,12,15,则以两个这样的三角形拼成的长方形的面积为__________.
中,若三边长分别为9,12,15,则以两个这样的三角形拼成的长方形的面积为__________.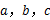 为△
为△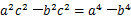 ,试判断△
,试判断△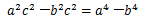 , ①
, ①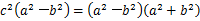 . ②
. ② . ③
. ③ ,则a的值是( )
,则a的值是( ) ;
;