题目内容
设方程2x2+3x=-1的根为x1、x2,求下列各式的值.
(1)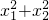 ;
;
(2) .
.
解:∵方程2x2+3x=-1的根为x1、x2,
∴x1+x2=- ,x1•x2=
,x1•x2= ,2x12+3x1=-1,
,2x12+3x1=-1,
(1)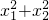
=(x1+x2)2-2x1x2
= -1
-1
= ;
;
(2)
=2 +3x1-(x1+x2)+3x1•x2
+3x1-(x1+x2)+3x1•x2
=-1+ +
+
=2.
分析:(1)首先根据原方程得到两根之和和两根之积,最后将代数式变形后代入即可求值;
(2)根据方程2x2+3x=-1的根为x1、x2,可得x1+x2=- ,x1•x2=
,x1•x2= ,2x12+3x1=-1,将原代数式变形为2
,2x12+3x1=-1,将原代数式变形为2 +3x1-(x1+x2)+3x1•x2后即可求值.
+3x1-(x1+x2)+3x1•x2后即可求值.
点评:本题考查了根与系数的关系,求出x1、x2的值再代入计算,则计算繁难,解题的关键是利用根与系数的关系及变形.
∴x1+x2=-
 ,x1•x2=
,x1•x2= ,2x12+3x1=-1,
,2x12+3x1=-1,(1)
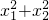
=(x1+x2)2-2x1x2
=
 -1
-1=
 ;
;(2)

=2
 +3x1-(x1+x2)+3x1•x2
+3x1-(x1+x2)+3x1•x2=-1+
 +
+
=2.
分析:(1)首先根据原方程得到两根之和和两根之积,最后将代数式变形后代入即可求值;
(2)根据方程2x2+3x=-1的根为x1、x2,可得x1+x2=-
 ,x1•x2=
,x1•x2= ,2x12+3x1=-1,将原代数式变形为2
,2x12+3x1=-1,将原代数式变形为2 +3x1-(x1+x2)+3x1•x2后即可求值.
+3x1-(x1+x2)+3x1•x2后即可求值.点评:本题考查了根与系数的关系,求出x1、x2的值再代入计算,则计算繁难,解题的关键是利用根与系数的关系及变形.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目