题目内容
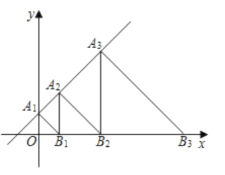
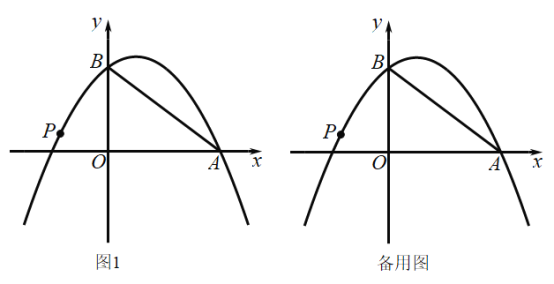
【题目】如图1,以直线![]() 为对称轴的抛物线
为对称轴的抛物线![]() 为常数)经过点A
为常数)经过点A![]() 和B
和B![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 是该抛物线上的一动点,设点
是该抛物线上的一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 是以
是以![]() 为直角边的直角三角形时,求
为直角边的直角三角形时,求![]() 的值;
的值;
②若![]() 满足
满足![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】![]() ;
;![]() ①
①![]() 或
或![]() ;②
;② ![]() 或
或![]()
【解析】
![]() 根据对称轴公式及经过两点列出关于a,b,c的方程,解方程即可得出答案;
根据对称轴公式及经过两点列出关于a,b,c的方程,解方程即可得出答案;
![]() ①分点B为直角顶点及点A为直角顶点,两种情况,得出两个三角形相似,即可得出答案;
①分点B为直角顶点及点A为直角顶点,两种情况,得出两个三角形相似,即可得出答案;
②分两种情况:![]() 在
在![]() 轴上找到
轴上找到![]() 记为点C,连接BC并延长交抛物线于点P,此时
记为点C,连接BC并延长交抛物线于点P,此时![]() ,求出直线BC解析式与抛物线联立即可得出点P的横坐标;
,求出直线BC解析式与抛物线联立即可得出点P的横坐标;![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,过点C作
,过点C作![]() 于E并延长交
于E并延长交![]() 于点
于点![]() ,根据勾股定理先求出
,根据勾股定理先求出![]() ,设点
,设点![]() ,再根据勾股定理求得a,b的值,得出
,再根据勾股定理求得a,b的值,得出![]() ,再与抛物线联立即可求得点P的横坐标.
,再与抛物线联立即可求得点P的横坐标.
![]()
![]()
![]() 是抛物线
是抛物线![]() 为常数)的对称轴,且经过点A
为常数)的对称轴,且经过点A![]() 和B
和B![]()

解得:
![]() 该抛物线的解析式为:
该抛物线的解析式为:![]()
![]() 设
设![]()

①![]() 若点B为直角顶点,作
若点B为直角顶点,作![]() ,
,![]() 交OB与点E
交OB与点E
易证![]()
![]()
即
解得:![]() 或
或![]() (舍去)
(舍去)
![]() 若点A为直角顶点,
若点A为直角顶点,![]() ,
,![]() 轴
轴
易证![]()
即
解得:![]() 或4(舍去)
或4(舍去)
②![]() 在
在![]() 轴上找到
轴上找到![]() 记为点C,连接BC并延长交抛物线于点P,此时
记为点C,连接BC并延长交抛物线于点P,此时![]()
设![]()
![]() 解析式过点
解析式过点![]() ,
,![]()
![]()
![]() 直线BC所在解析式为
直线BC所在解析式为![]()

解得:![]() 或
或![]() (舍去)
(舍去)
![]()
![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,过点C作
,过点C作![]() 于E并延长交
于E并延长交![]() 于点
于点![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
即![]()
将①②联立解得:![]()
设![]() ,则点
,则点![]()
![]()
![]()
![]()
将①②联立解得:![]()
![]()
设![]() 直线解析式为:
直线解析式为:![]()


![]()

解得:![]() 或
或![]() (舍去)
(舍去)
![]()


练习册系列答案
相关题目
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
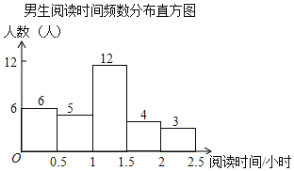
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?