题目内容
如图，△ABC的顶点都在方格纸的格点上，则sinC=
| ||
| 10 |
| ||
| 10 |
分析：根据网格结构连接格点AD、BD，利用勾股定理列式求出AC2、AD2、CD2，再利用勾股定理逆定理判断出△ACD是直角三角形，然后根据锐角的正弦等于对边比斜边列式计算即可得解．
解答：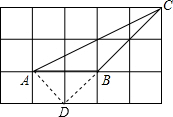
解：如图，连接格点AD、BD，
由勾股定理得，AC2=22+42=20，
AD2=12+12=2，
CD2=32+32=18，
∵AD2+CD2=AC2，
∴△ACD是直角三角形，
∴sinC=
=
=
．
故答案为：
．
解：如图，连接格点AD、BD，由勾股定理得，AC2=22+42=20，
AD2=12+12=2，
CD2=32+32=18，
∵AD2+CD2=AC2，
∴△ACD是直角三角形，
∴sinC=
| AD |
| AC |
| ||
|
| ||
| 10 |
故答案为：
| ||
| 10 |
点评：本题考查了勾股定理，锐角三角函数的定义，熟练掌握网格结构，作辅助线构造成直角三角形是解题的关键．
练习册系列答案
相关题目
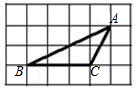如图，△ABC的顶点都是正方形网格中的格点，则sin∠ABC等于
如图，△ABC的顶点坐标分别为A （ 3，6 ），B （ 1，3 ），C （ 4，2 ）．如果将△ABC绕C点顺时针旋转90°，得到△A′B′C′，那么点A的对应点A′的坐标为
如图，△ABC的顶点坐标分别为A（1，3）、B（4，2）、C（2，1）．
如图，△ABC的顶点都在方格纸的格点上，将△ABC向左平移2格，再向上平移2格，其中每个格子的边长为1个单位长度．