题目内容
 (2012•岱岳区二模)如图,一次函数y=-
(2012•岱岳区二模)如图,一次函数y=-
| ||
| 3 |
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(a,
| 1 |
| 2 |
分析:(1)首先令x=0,y=0求出一次函数的解析式.然后根据勾股定理求出AB的长,继而可求出三角形ABC的面积.
(2)依题意可得出S四边形ABPO=S△ABO+S△BOP,当S△ABP=S△ABC时求出a值.
(2)依题意可得出S四边形ABPO=S△ABO+S△BOP,当S△ABP=S△ABC时求出a值.
解答:解:(1)y=-
x+1与x轴、y轴交于A、B两点,
∴A(
,0),B(0,1).
∵△AOB为直角三角形,
∴AB=2.
∴S△ABC=
×2×sin60°=
.
(2)S四边形ABPO=S△ABO+S△BOP=
×OA×OB+
×OB×h=
×
×1+
×1×|a|.
∵P在第二象限,∴S四边形ABPO=
-
=
,
S△ABP=SABPO-S△AOP=(
-
)-
×OA×
.
∴S△ABP=
-
-
=
-
=S△ABC=
.
∴a=-
.
| ||
| 3 |
∴A(
| 3 |
∵△AOB为直角三角形,
∴AB=2.
∴S△ABC=
| 1 |
| 2 |
| 3 |
(2)S四边形ABPO=S△ABO+S△BOP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
∵P在第二象限,∴S四边形ABPO=
| ||
| 2 |
| a |
| 2 |
| ||
| 2 |
S△ABP=SABPO-S△AOP=(
| ||
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABP=
| ||
| 2 |
| a |
| 2 |
| ||
| 4 |
| ||
| 4 |
| a |
| 2 |
| 3 |
∴a=-
3
| ||
| 2 |
点评:本题考查了一次函数的综合运用以及三角形的面积计算等知识,重点考查考生利用数形结合解题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
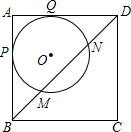 (2012•岱岳区二模)半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2
(2012•岱岳区二模)半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2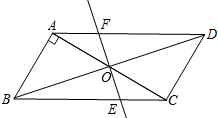 (2012•岱岳区二模)已知,如图,平行四边形ABCD中,AB⊥AC,
(2012•岱岳区二模)已知,如图,平行四边形ABCD中,AB⊥AC, (2012•岱岳区二模)四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么cosθ的值是
(2012•岱岳区二模)四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么cosθ的值是