题目内容
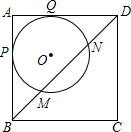 (2012•岱岳区二模)半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2
(2012•岱岳区二模)半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2| 3 |
4+
或4-
| 2 |
| 2 |
4+
或4-
.| 2 |
| 2 |
分析:首先取BD的中点E,连接AE,OM,ON,OP,OQ,由BD是正方形ABCD的对角线,可得AE⊥BD,又由⊙O与正方形ABCD相切于点P、Q,证得四边形APOQ是正方形,根据切线长定理,可得AE过圆心O,则可求得OE与OA的长,可得AE的长,继而求得答案,解题时注意对圆心位置的讨论.
解答: 解:①当圆心O在对角线BD的上方时,
解:①当圆心O在对角线BD的上方时,
取BD的中点E,连接AE,OM,ON,OP,OQ,
∵BD是正方形ABCD的对角线,
∴AE⊥BD,
∵⊙O与正方形ABCD相切于点P、Q,
∴OP⊥AB,OQ⊥AD,
∵OP=OQ,
∴四边形APOQ是正方形,
∴OA=
OQ=2
,
∴∠QAE=∠PAE,
∴AE过⊙O的圆心O,
∴OE⊥BD,
∵OM=ON=2,MN=2
,
∴OE=1,
∴AE=OA+OE=2
+1,
∴AB=
=
AE=4+2
,
②当圆心O在对角线BD的下方时,
有①可知AE=OA-OE=2
-1,
∴AB=
=
AE=4-2
故答案为:4+2
或4-2
.
 解:①当圆心O在对角线BD的上方时,
解:①当圆心O在对角线BD的上方时,取BD的中点E,连接AE,OM,ON,OP,OQ,
∵BD是正方形ABCD的对角线,
∴AE⊥BD,
∵⊙O与正方形ABCD相切于点P、Q,
∴OP⊥AB,OQ⊥AD,
∵OP=OQ,
∴四边形APOQ是正方形,
∴OA=
| 2 |
| 2 |
∴∠QAE=∠PAE,
∴AE过⊙O的圆心O,
∴OE⊥BD,
∵OM=ON=2,MN=2
| 3 |
∴OE=1,
∴AE=OA+OE=2
| 2 |
∴AB=
| AE |
| sin45° |
| 2 |
| 2 |
②当圆心O在对角线BD的下方时,
有①可知AE=OA-OE=2
| 2 |
∴AB=
| AE |
| sin45° |
| 2 |
| 2 |
故答案为:4+2
| 2 |
| 2 |
点评:此题考查了切线的性质、正方形的判定与性质、切线长定理以及三角函数等知识.此题综合性较强,难度较大,解题的关键是准确作出辅助线,利用数形结合思想求解.

练习册系列答案
相关题目
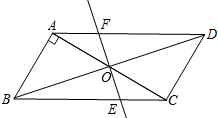 (2012•岱岳区二模)已知,如图,平行四边形ABCD中,AB⊥AC,
(2012•岱岳区二模)已知,如图,平行四边形ABCD中,AB⊥AC, (2012•岱岳区二模)四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么cosθ的值是
(2012•岱岳区二模)四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么cosθ的值是