题目内容
在⊙O中，弦AC、BD相交于点E，且弧AB=BC，弧BC=CD，若∠BEC=130°，则∠ACD的度数为
- A.150
- B.30°
- C.80°
- D.105°
D
分析：根据等弧对等角及等边对等角可得到∠BAC=∠BCA=∠CBD=∠CDB，再根据三角形外角的性质及三角形内角和定理求解即可．
解答：∵弧AB=弧BC，弧BC=弧CD
∴AB=BC=CD
∴∠BAC=∠BCA=∠CBD=∠CDB
∵∠BEC=130°
∴∠BCA=∠CBD=25°，∠CED=50°
∴∠ACD=180°-50°-25°=105°．
故选D．
点评：综合运用圆周角定理和三角形的内角和定理．
分析：根据等弧对等角及等边对等角可得到∠BAC=∠BCA=∠CBD=∠CDB，再根据三角形外角的性质及三角形内角和定理求解即可．
解答：∵弧AB=弧BC，弧BC=弧CD
∴AB=BC=CD
∴∠BAC=∠BCA=∠CBD=∠CDB
∵∠BEC=130°
∴∠BCA=∠CBD=25°，∠CED=50°
∴∠ACD=180°-50°-25°=105°．
故选D．
点评：综合运用圆周角定理和三角形的内角和定理．
练习册系列答案
相关题目
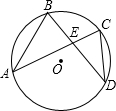如图，在⊙O中，弦AC与BD交于E，AB=6，AE=8，ED=4，求CD的长．
16、在⊙O中，弦AC、BD相交于点E，且弧AB=BC，弧BC=CD，若∠BEC=130°，则∠ACD的度数为（ ）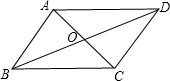
（1）如图，在?ABCD中，对角线AC、BD相交于点O．请找出图中的一对全等三角形，并给予证明；
如图，在⊙O中，弦AC和BD相交于点E，
如图，在⊙O中，弦AC、BD相交于点P，已知弧AB、弧CD所对的圆心角的度数分别为65°和45°，则∠APB=