题目内容
如图，已知CD=6cm，AD=8cm，∠ADC=90°，BC=24cm，AB=26cm，求四边形ABCD的面积．
解：∵CD=6cm，AD=8cm，∠ADC=90°，
∴AC=
=10cm．
∵102+242=262．
∴△ABC为直角三角形，∠ACB=90°．
∴四边形ABCD的面积=S△ABC-S△ACD=
×10×24-×6×8=96．
分析：根据勾股定理可求出AC的长，根据勾股定理的逆定理可求出∠ACB=90°，可求出△ACB的面积，减去△ACD的面积，可求出四边形ABCD的面积．
点评：本题考查了勾股定理和勾股定理的逆定理，关键判断出直角三角形从而可求出面积．
∴AC=
=10cm．∵102+242=262．
∴△ABC为直角三角形，∠ACB=90°．
∴四边形ABCD的面积=S△ABC-S△ACD=
×10×24-×6×8=96．分析：根据勾股定理可求出AC的长，根据勾股定理的逆定理可求出∠ACB=90°，可求出△ACB的面积，减去△ACD的面积，可求出四边形ABCD的面积．
点评：本题考查了勾股定理和勾股定理的逆定理，关键判断出直角三角形从而可求出面积．
练习册系列答案
教学练新同步练习系列答案
相关题目
14、如图，已知AB∥CD，EF∥HG，则图中与∠1互补的角共有（ ）个．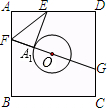
如图，已知正方形纸片ABCD的边长为8，O是正方形的中心，⊙O的半径为2．沿EF折叠纸片，使点A落在⊙O上的A1处，且EA1所在直线与⊙O只有一个公共点A1，延长FA1交CD边于点G，则A1G的长是（ ）
如图，已知D、E为△ABC的边AB、AC上的点，BE⊥AC，CD⊥AB，BE、DC相交于点O，则图中相似三角形对数为（ ）
如图，已知四边形ABCD，对角线AC，BD相交于点O．仅从下列六项条件中任意选取两项作为已知条件，就能够确定四边形ABCD是平行四边形的方法有（ ）种
