题目内容
已知AD是△ABC的高,∠BAD=70゜,∠CAD=20゜,求∠BAC的度数.
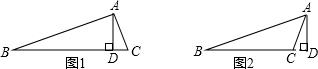 解:①如图1,当高AD在△ABC的内部时,
解:①如图1,当高AD在△ABC的内部时,∠BAC=∠BAD+∠CAD=70°+20°=90°;
②如图2,当高AD在△ABC的外部时,
∠BAC=∠BAD-∠CAD=70°-20°=50°,
综上所述,∠BAC的度数为90°或50°.
分析:分高AD在△ABC内部和外部两种情况讨论求解即可.
点评:本题考查了三角形的高线,难点在于要分情况讨论.

练习册系列答案
相关题目
题目内容
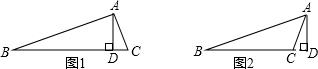 解:①如图1,当高AD在△ABC的内部时,
解:①如图1,当高AD在△ABC的内部时,