题目内容
2．已知二元一次方程3x-y=5，给出下列变形：①y=3x+5，②x=$\frac{y+5}{3}$，③-6x+2y=-10，其中正确的是（ ）| A． | ② | B． | ①② | C． | ①③ | D． | ②③ |
分析 已知方程变形得到结果，即可做出判断．
解答 解：方程3x-y=5，
解得：y=3x-5，x=$\frac{y+5}{3}$，-6x+2y=-10，
其中正确的为②③，
故选D
点评 此题考查了解二元一次方程，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
12．计算：
（1）x3÷（x2）3÷x5
（2）（x+1）（x-3）+x（2-x）
（3）（-$\frac{1}{3}$）0+（$\frac{1}{2}$）-2+（0.2）2015×52015-|-1|
（1）x3÷（x2）3÷x5
（2）（x+1）（x-3）+x（2-x）
（3）（-$\frac{1}{3}$）0+（$\frac{1}{2}$）-2+（0.2）2015×52015-|-1|
10．若分式$\frac{{x}^{2}-9}{6-2x}$的值为0，则x的值为（ ）
| A． | 0 | B． | 3或-3 | C． | 3 | D． | -3 |
7．下列分式运算或化简错误的是（ ）
| A． | $\frac{1-3x}{-x-2}$=$\frac{3x-1}{x+2}$ | B． | $\frac{-2{x}^{3}y}{4{x}^{2}{y}^{2}}$=-$\frac{x}{2y}$ | ||
| C． | （x2-xy）÷$\frac{x-y}{x}$=（x-y）2 | D． | $\frac{4}{x-2}$+$\frac{x+2}{2-x}$=-1 |
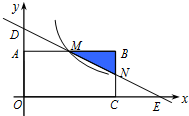如图，在直角坐标系中，长方形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为（4，2）．过点D（0，3）和E（6，0）的直线分别与AB，BC交于点M，N．