题目内容
直角三角形ABC的三条边长是三个连续的偶数，圆O是△ABC的内切圆．在△ABC外部将圆O沿△ABC的边滚动一周，则圆O滚动一周所扫过的面积是________．
96+16π
分析：设三角形的三边长分别为x，x+2，x+4，内切圆的半径为r，根据勾股定理和切线的性质可求得x与r，圆O滚动一周所扫过的图形是三个矩形和三个扇形，再求面积即可．
解答：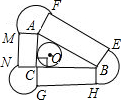
解：如图，设三角形的三边长分别为x，x+2，x+4，内切圆的半径为r，
则x2+（x+2）2=（x+4）2，
解得x=6，
∴三角形的三边长分别为6、8、10，
∴由切线的性质得6-r+8-r=10，
∴r=2，
∴圆O滚动一周所扫过的图形是三个矩形即ABEF，BCGH，ACMN和三个扇形MAF，EBH，GCN，
∴圆O滚动一周所扫过的面积是 4×10+4×8+4×6+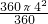
=96+16π．
故答案为：96+16π．
点评：本题考查了三角形的内切圆和内心，勾股定理、和扇形面积的计算，找出圆O滚动一周所扫过的图形是解题的关键．
分析：设三角形的三边长分别为x，x+2，x+4，内切圆的半径为r，根据勾股定理和切线的性质可求得x与r，圆O滚动一周所扫过的图形是三个矩形和三个扇形，再求面积即可．
解答：
解：如图，设三角形的三边长分别为x，x+2，x+4，内切圆的半径为r，则x2+（x+2）2=（x+4）2，
解得x=6，
∴三角形的三边长分别为6、8、10，
∴由切线的性质得6-r+8-r=10，
∴r=2，
∴圆O滚动一周所扫过的图形是三个矩形即ABEF，BCGH，ACMN和三个扇形MAF，EBH，GCN，
∴圆O滚动一周所扫过的面积是 4×10+4×8+4×6+
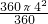=96+16π．故答案为：96+16π．
点评：本题考查了三角形的内切圆和内心，勾股定理、和扇形面积的计算，找出圆O滚动一周所扫过的图形是解题的关键．
练习册系列答案
相关题目
如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．已知直角三角形ABC的三个顶点都在格点上．