题目内容
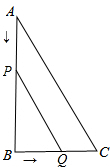 如图,在△ABC中,∠B=90°,AB=22cm,BC=20cm.点P从点A开始沿AB边点B以2cm/s的速度移动,点Q从点B以1cm/s的速度向点C移动,且P、Q两点分别从A、B两点同时出发.
如图,在△ABC中,∠B=90°,AB=22cm,BC=20cm.点P从点A开始沿AB边点B以2cm/s的速度移动,点Q从点B以1cm/s的速度向点C移动,且P、Q两点分别从A、B两点同时出发.(1)求四边形APQC面积y(cm2)与运动时间x(s)之间的函数关系式,并写出x的取值范围;
(2)求四边形APQC面积最小值,并求出此时x的值.
考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:(1)易求得AP,BQ的长,即可求得BP的长,根据四边形APQC面积y(cm2)=S△ABC-S△BPQ即可解题;
(2)根据(1)中二次函数式求得最小值即可解题.
(2)根据(1)中二次函数式求得最小值即可解题.
解答:解:(1)∵x秒后AP=2x,BQ=x,
∴BP=AB-AP=22-2x,
∴S△BPQ=
BP•BQ=x(11-x)cm2,
∵S△ABC=
AB•BC=220cm2,
∴四边形APQC面积y(cm2)=S△ABC-S△BPQ=220-x(11-x)=x2-11x+220;
(2)y=x2-11x+220,
当x=-
=
时,y有最小值为
.
∴BP=AB-AP=22-2x,
∴S△BPQ=
| 1 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
∴四边形APQC面积y(cm2)=S△ABC-S△BPQ=220-x(11-x)=x2-11x+220;
(2)y=x2-11x+220,
当x=-
| b |
| 2a |
| 11 |
| 2 |
| 759 |
| 4 |
点评:本题考查了二次函数解析式的求解,考查了二次函数最值的求解,本题中求的BP的长是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
郑州地铁,是郑州市第一个轨道运输系统.根据规划,由六条线路组成,预计总投资1000亿元.1000亿元用科学记数法表示为(保留两个有效数字)( )
| A、1×1010元 |
| B、1×1011元 |
| C、1.0×1010元 |
| D、1.0×1011元 |
 如图,是一块电脑主板的示意图(单位:mm),其中每个角都是直角,则这块主板的周长是
如图,是一块电脑主板的示意图(单位:mm),其中每个角都是直角,则这块主板的周长是 如图,直线a∥b,则∠A的度数是
如图,直线a∥b,则∠A的度数是