题目内容
(本题满分10分)
猜想与证明:
如图1摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.

拓展与延伸:
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.
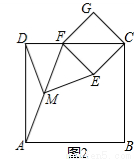
猜想与证明:DM=ME;拓展与延伸:(1)DM=ME.(2)成立,见解析.
【解析】
试题分析:猜想与证明:观察图形可猜想DM=ME;延长EM交AD于点H,只需证明HM=EM,利用直角三角形的性质便可证明HM=DM=EM,因此根据条件证明△FME≌△AMH即可;拓展与延伸:(1)观察图形可得出结论:DM=ME;(2)连接AE,说明△AEF是直角三角形,利用直角三角形斜边上的中线等于斜边的一半,可得ME=MF=MA,得证.
试题解析:
【解析】
猜想:DM=ME
证明:如图1,延长EM交AD于点H,

∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,

∴△FME≌△AMH(ASA)∴HM=EM,
在RT△HDE中,HM=EM,∴DM=HM=ME,∴DM=ME.
(1)如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,
∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,
∴△FME≌△AMH(ASA)∴HM=EM,
在RT△HDE中,HM=EM,∴DM=HM=ME,∴DM=ME,故答案为:DM=ME.
(2)如图2,连接AE,

∵四边形ABCD和ECGF是正方形,∴∠FCE=45°,∠FCA=45°,
∴AE和EC在同一条直线上,在RT△ADF中,AM=MF,∴DM=AM=MF,
在RT△AEF中,AM=MF,∴AM=MF=ME, ∴DM=ME.
考点:1.矩形的性质;2.正方形的性质;3.全等三角形的判定与性质;4.直角三角形的性质.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性- 题型:
- 难度:
- 考核:
- 年级:


 只同一型号的零件,他们生产的零件
只同一型号的零件,他们生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
(分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
 倍,请分别求出甲、乙两人生产全过程中,生产的零件
倍,请分别求出甲、乙两人生产全过程中,生产的零件 (分)的函数关系式;
(分)的函数关系式;
 中,
中, ,
, ,
, ,则
,则 = .
= . 位观众,将
位观众,将 用科学记数法表示为( )
用科学记数法表示为( ) B.
B. C.
C. D.
D.
 .
. ,
, ,且
,且 +3
+3 =3,求m的值。
=3,求m的值。 的值为负数,则x的取值范围是 .
的值为负数,则x的取值范围是 . 的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-2,0),点A的横坐标是2,tan∠CDO=
的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-2,0),点A的横坐标是2,tan∠CDO= .
.
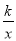 恰好经过BC的中点E,则k的值( )
恰好经过BC的中点E,则k的值( )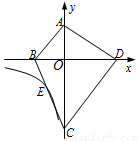
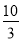 B.-
B.-