题目内容
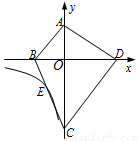
如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为10和20,若双曲线y=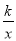 恰好经过BC的中点E,则k的值( )
恰好经过BC的中点E,则k的值( )
A.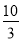 B.-
B.-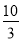 C.5 D.-5
C.5 D.-5
A
【解析】
试题分析:∵AB∥CD,设AO:BO=OC:OD=m,OC:OA=OD:OB=n 则PA=m·OB,OC=n·OA=mn·OB,OD=n·OB
根据三角形的面积可得: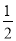 m·(n+1)·
m·(n+1)·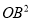 =10;
=10;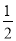 mn·(n+1)·
mn·(n+1)·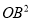 =20,两式相除可得:n=2
=20,两式相除可得:n=2
将n=2代入可得:m·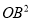 =
=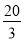 ,根据中点可得点E的坐标为(-
,根据中点可得点E的坐标为(-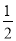 OB,-
OB,-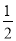 OC),则k=-
OC),则k=-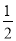 OB·(-
OB·(-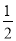 OC)=
OC)=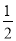 ·m·
·m·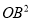 =
=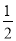 ×
×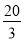 =
=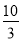 .
.
考点:反比例函数的性质.
考点分析: 考点1:反比例函数 一般地,函数 (k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。
(k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。 注:
(1)因为分母不能为零,所以反比例函数函数的自变量x不能为零,同样y也不能为零;
(2)由
 ,所以反比例函数可以写成
,所以反比例函数可以写成 的形式,自变量x的次数为-1;
的形式,自变量x的次数为-1; (3)在反比例函数中,两个变量成反比例关系,即
 ,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。
,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。表达式:
x是自变量,y是因变量,y是x的函数
 自变量的取值范围:
自变量的取值范围:①在一般的情况下,自变量x的取值范围可以是不等于0的任意实数;
②函数y的取值范围也是任意非零实数。 反比例函数性质:
①反比例函数的表达式中,等号左边是函数值y,等号右边是关于自变量x的分式,分子是不为零的常数k,分母不能是多项式,只能是x的一次单项式;
②反比例函数表达式中,常数(也叫比例系数)k≠0是反比例函数定义的一个重要组成部分;
③反比例函数
 (k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
试题属性
(k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目



 =0的根的情况是( )
=0的根的情况是( )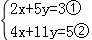 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法: .
.
 .
.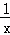 +
+ 的值.
的值.