题目内容
3.试说明,对于任意一个正整数n,代数式(n+5)2-(n-7)2的值一定是24的倍数.分析 原式利用平方差公式分解,即可做出判断.
解答 解:(n+5)2-(n-7)2=(n+5+n-7)(n+5-n+7)=12(2n-2)=24(n-1),
则对于任意一个正整数n,代数式(n+5)2-(n-7)2的值一定是24的倍数.
点评 此题考查了因式分解-运用公式法,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
13.符合条件∠A+∠B=∠C的△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
15.“比a的$\frac{3}{2}$倍大1的数”用式子表示为( )
| A. | $\frac{2}{3}$a+1 | B. | $\frac{3}{2}$a+1 | C. | $\frac{5}{2}$a | D. | $\frac{3}{2}$a-1 |
13.若k为任意实数,则抛物线y=-2(x-k)2+k2的顶点在( )
| A. | 抛物线y=x2上 | B. | 直线y=-x上 | C. | x轴上 | D. | y轴上 |
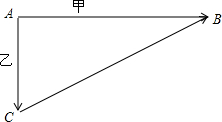 甲、乙两只渔船同时从一渔港(A)出发,甲船向正东方向航行,速度是8海里/小时,乙船向正南方向航行,速度是6海里/小时,2小时后,甲船到达B处,乙船到达C处.
甲、乙两只渔船同时从一渔港(A)出发,甲船向正东方向航行,速度是8海里/小时,乙船向正南方向航行,速度是6海里/小时,2小时后,甲船到达B处,乙船到达C处.