题目内容
【题目】如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)△BDE可由△ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法).
【答案】
(1)证明:在Rt△ABC中,
∵∠ABC=90°,
∴∠ABE+∠DBE=90°,
∵BE⊥AC,
∴∠ABE+∠A=90°,
∴∠A=∠DBE,
∵DE是BD的垂线,
∴∠D=90°,
在△ABC和△BDE中,
∵ 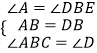 ,
,
∴△ABC≌△BDE(ASA)
(2)解:如图①,点O就是所求的旋转中心.

作法二:如图②,点O就是所求的旋转中心.

【解析】(1)要证△ABC≌△BDE,由已知可知有一组直角相等和一组对应边相等,还需证明一组对应角相等。根据同角的余角相等,即可得证。
(2)方法一、作AB、BD的垂直平分线,两垂直平分线的交点就是旋转中心;方法二、以AB、BD为邻边作正方形,正方形对角线的交点就是所求作的旋转中心。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】某电器超市销售每台进价为120元、170元的A,B两种型号的电风扇,如表所示是近2周的销售情况:(进价、售价均保持不变,利润=销售收入一进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 6 | 5 | 2200元 |
第二周 | 4 | 10 | 3200元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市再采购这两种型号的电风扇共130台,并且全部销售完,该超市能否实现这两批的总利润为8010元的目标?若能,请给出相应的采购方案;若不能,请说明理由.