题目内容
19．
如图，在五边形ABCDE中，∠B=∠E，AB=AE，BC=ED，AM⊥CD于M，求证：CM=MD．
分析 如图，连接AC、AD，证明△ABC≌△AED，得到AC=AD，利用定义三角形的性质，根据AM⊥CD于M，得到CM=MD．
解答 解：如图，连接AC、AD，
在△ABC和△AED中，
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=ED}\end{array}\right.$
∴△ABC≌△AED，
∴AC=AD，
∵AM⊥CD于M，
∴CM=MD．
点评 本题主要考查了全等三角形的判定及性质、等腰三角形的性质，解决本题的关键是连接AC、AD，证明△ABC≌△AED，得到AC=AD．
练习册系列答案
名校课堂系列答案
相关题目
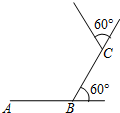如图，小东在操场的中心位置，从点A出发，每走6m向左转60°，
如图，在∠AOB内部一找P，使点P到OA和BO的距离相等，且到点O的距离等于2.5厘米，请你在图中找出这个点．
如图，已知线段a，b，求作：线段x，使x=$\frac{{a}^{2}}{b}$．