题目内容
【题目】在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在
上的所有点都在![]() 的内部或边长,则称
的内部或边长,则称![]() 为
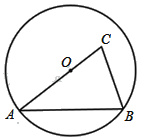
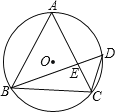
为![]() 的中内弧.例如下图中
的中内弧.例如下图中![]() 是
是![]() 的一条中内弧.
的一条中内弧.
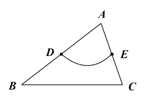
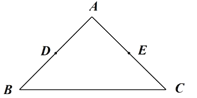
(1)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.画出
的中点.画出![]() 的最长的中内弧
的最长的中内弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点.
的中点.
①若![]() ,直接写出
,直接写出![]() 的中内弧
的中内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标
的纵坐标![]() 的取值范围;
的取值范围;
②若在![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长,直接写出
的内部或边长,直接写出![]() 的取值范围;
的取值范围;
③若在![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长,则
的内部或边长,则![]() 的最小值为__________.
的最小值为__________.
【答案】(1)图见解析,![]() ;(2)①
;(2)①![]() 或
或![]() ;②
;②![]() ;③
;③![]()
【解析】
(1)先根据中内弧的概念确认![]() 最长时圆的位置,再根据等腰直角三角形、勾股定理求解即可;
最长时圆的位置,再根据等腰直角三角形、勾股定理求解即可;
(2)①结合(1)中的结论确定中内弧![]() 为最长弧时的位置,从而得到临界位置,再利用数形结合确定点P的纵坐标的取值范围即可;
为最长弧时的位置,从而得到临界位置,再利用数形结合确定点P的纵坐标的取值范围即可;
②先分别求出点P在两个临界位置(即在x轴上和在BC上)时t的值,再根据中内弧的定义、相似三角形的判定与性质即可得出t的取值范围;
③先参照②的方法,求出t的取值范围,再根据三角函数值求出![]() ,然后根据二次函数的性质求出
,然后根据二次函数的性质求出![]() 的取值范围,从而可得出答案.
的取值范围,从而可得出答案.
(1)由题意可知,![]() 的圆心在DE的垂直平分线上,即在BC的垂直平分线上,当圆心为DE的中点时,
的圆心在DE的垂直平分线上,即在BC的垂直平分线上,当圆心为DE的中点时,![]() 与BC相切,此时
与BC相切,此时![]() 是
是![]() 的最长的中内弧
的最长的中内弧
![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点
的中点
![]()
![]()
![]() 所在圆的半径为
所在圆的半径为![]()
则![]() 的长为
的长为![]() ;
;
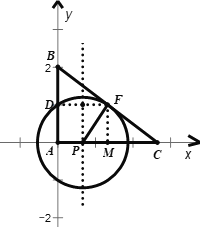
(2)①如图,当![]() 时,
时,![]()
则![]()
由题意知,中内弧![]() 所在圆的圆心
所在圆的圆心![]() 在DF的垂直平分线PQ上,即在
在DF的垂直平分线PQ上,即在![]() 上
上
分以下两种情况:
当中内弧![]() 在DF下方时
在DF下方时
由(1)可知,当P为DF中点时是一个临界位置
此时,点P坐标为![]()
由中内弧的定义可知,当点P纵坐标![]() 时,所有的
时,所有的![]() 都是中内弧
都是中内弧
当中内弧![]() 在DF上方时
在DF上方时
圆P与BC相切是一个临界位置,此时![]()
![]()
![]()
由中位线定理得![]()
![]()
![]()
![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]() ,即
,即![]()
由中内弧的定义可知,当点P纵坐标![]() 时,所有的
时,所有的![]() 都是中内弧
都是中内弧
综上,纵坐标![]() 的取值范围为
的取值范围为![]() 或
或![]() ;
;

②![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点
的中点
![]()
如图,当点P在AC上,且圆P与BC相切于点F时,则![]()
过点F作![]()
![]()
![]()
又![]()
![]()
![]() ,即
,即![]()
解得![]() 或
或![]() (舍去)
(舍去)
则当![]() 时,
时,![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长
的内部或边长
如图,当点P在BC上时,圆P与AC相切于点N,则![]()
![]()
![]() ,即
,即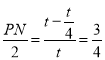
![]()
![]()
![]()
![]() ,即
,即![]()
解得![]()
则当![]() 时,
时,![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长
的内部或边长
综上,所求的t的取值范围为![]() ;
;
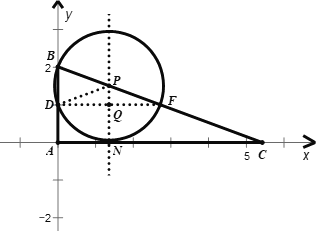
③![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点
的中点
![]()
如图,当点Q在AC上,且圆Q与BC相切于点G,连接DQ
设![]() ,则
,则![]()
![]()
![]()
![]() ,即
,即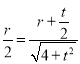
解得![]()
在![]() 中,
中,![]() ,即
,即![]()
将![]() 代入解得:
代入解得:![]() (其中,负值不符题意,舍去)
(其中,负值不符题意,舍去)
则当![]() 时,
时,![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长
的内部或边长

如图,当点Q在BC上时,圆Q与![]() 分别相切于点
分别相切于点![]() ,连接
,连接![]()
则四边形ADQE是正方形,![]()
由中位线定理得![]()
![]() ,解得
,解得![]()
则当![]() 时,
时,![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长
的内部或边长
综上,t的取值范围为![]()
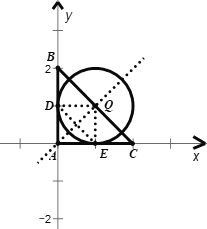
![]()
要使![]() 的最小,则
的最小,则![]() 要取得最大值
要取得最大值
由二次函数的性质可知,当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
则当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]()
因此,![]() 的最小值为
的最小值为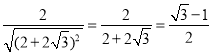 .
.

【题目】某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | … |
x(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
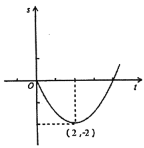
(1)如果y是t的函数,
①如图,在平面直角坐标系tOy中,描出了上表中y与t各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
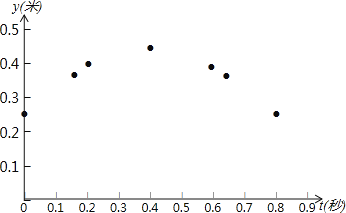
②当t为何值时,乒乓球达到最大高度?
(2)如果y是关于x的二次函数,那么乒乓球第一次落在桌面时,与端点A的水平距离是多少?