题目内容
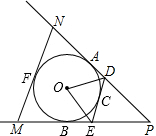 如图,P是⊙O外一点,PA、PB分别和相⊙O切于点A、B,C是劣弧
如图,P是⊙O外一点,PA、PB分别和相⊙O切于点A、B,C是劣弧 |
| AB |
(1)求∠P的度数;
(2)求PA的长;
(3)求四边形DEMN的周长.
考点:圆的综合题
专题:
分析:(1)连接OA、OB,根据切线长定理和切线定理可推出∠AOD=∠COD,∠COE=∠BOE,从而可求出∠AOB,在四边形PAOB中,利用四边形内角和定理就可求出∠P.
(2)根据切线长定理可得到DA=DC,EC=EB,PA=PB,从而可得到C△PDE=2PA,根据条件就可求出PA的长.
(3)根据切线长定理可得到NA=NF,MF=MB,EB=EC,DA=DC,从而得到MN+DE=ND+EM.然后只需根据根与系数的关系求出DN+EM的值,就可解决问题.
(2)根据切线长定理可得到DA=DC,EC=EB,PA=PB,从而可得到C△PDE=2PA,根据条件就可求出PA的长.
(3)根据切线长定理可得到NA=NF,MF=MB,EB=EC,DA=DC,从而得到MN+DE=ND+EM.然后只需根据根与系数的关系求出DN+EM的值,就可解决问题.
解答:解:(1)连接OA、OB,如图.
∵PA、PB、DE分别和⊙O相切于点A、B、C,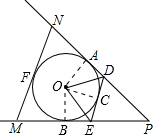
∴∠ADO=∠CDO,∠CEO=∠BEO,
∠OAD=∠OCD=∠OCE=∠OBE=90°,
∴∠AOD=∠COD,∠COE=∠BOE,
∴∠AOB=2∠DOE=2×70°=140°,
∴∠P=360°-∠OAP-∠OBP-∠AOB=40°.
(2)∵PA、PB、DE分别和⊙O相切于点A、B、C,
∴DA=DC,EC=EB,PA=PB,
∴C△PDE=PD+DE+PE=PD+DC+CE+PE=PD+DA+BE+PE=PA+PB=2PA,
∵C△PDE=8,∴PA=4,
∴PA的长为4cm.
(3)∵PN、PM、DE、MN分别和⊙O相切于点A、B、C、F,
∴NA=NF,MF=MB,EB=EC,DA=DC,
∴MN+DE=NF+MF+DC+EC=NA+MB+DA+EB=ND+EM.
∵DN、EM的长是方程x2-10x+k=0的两根,
∴DN+EM=10,∴MN+DE=10,
∴四边形DEMN的周长为20.
∵PA、PB、DE分别和⊙O相切于点A、B、C,

∴∠ADO=∠CDO,∠CEO=∠BEO,
∠OAD=∠OCD=∠OCE=∠OBE=90°,
∴∠AOD=∠COD,∠COE=∠BOE,
∴∠AOB=2∠DOE=2×70°=140°,
∴∠P=360°-∠OAP-∠OBP-∠AOB=40°.
(2)∵PA、PB、DE分别和⊙O相切于点A、B、C,
∴DA=DC,EC=EB,PA=PB,
∴C△PDE=PD+DE+PE=PD+DC+CE+PE=PD+DA+BE+PE=PA+PB=2PA,
∵C△PDE=8,∴PA=4,
∴PA的长为4cm.
(3)∵PN、PM、DE、MN分别和⊙O相切于点A、B、C、F,
∴NA=NF,MF=MB,EB=EC,DA=DC,
∴MN+DE=NF+MF+DC+EC=NA+MB+DA+EB=ND+EM.
∵DN、EM的长是方程x2-10x+k=0的两根,
∴DN+EM=10,∴MN+DE=10,
∴四边形DEMN的周长为20.
点评:本题主要考查了切线长定理和切线的性质、四边形的内角和定理、根与系数的关系、等角的余角相等等知识,运用切线的性质和切线长定理是解决本题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目

 一艘轮船以18海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°的方向上,两小时后,轮船在B处测得小岛P在北偏西30°的方向上,已知小岛周围20海里内有暗礁,若轮船仍按原来方向继续前行,有无触礁的危险?
一艘轮船以18海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°的方向上,两小时后,轮船在B处测得小岛P在北偏西30°的方向上,已知小岛周围20海里内有暗礁,若轮船仍按原来方向继续前行,有无触礁的危险?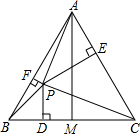 如图,P是等边△ABC内任意一点,由P向边BC、AC、AB分别引垂线段PD、PE、PF,AM⊥BC,AM=6cm,则PD+PE+PF=
如图,P是等边△ABC内任意一点,由P向边BC、AC、AB分别引垂线段PD、PE、PF,AM⊥BC,AM=6cm,则PD+PE+PF=