题目内容
14.我市东坡实验中学准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必选且只能选择这五项活动中的一种).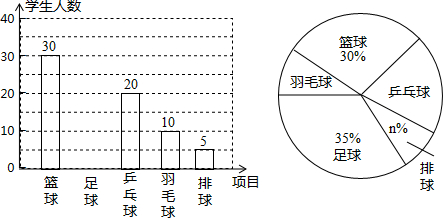
根据以上统计图提供的信息,请解答下列问题:
(1)m=100,n=5.
(2)补全上图中的条形统计图.
(3)若全校共有2000名学生,请求出该校约有多少名学生喜爱打乒乓球.
(4)在抽查的m名学生中,有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母A、B、C、D代表)
分析 (1)篮球30人占30%,可得总人数,由此可以计算出n;
(2)求出足球人数=100-30-20-10-5=35人,即可解决问题;
(3)用样本估计总体的思想即可解决问题.
(4)画出树状图即可解决问题.
解答 解:(1)由题意m=30÷30%=100,排球占$\frac{5}{100}$=5%,
∴n=5,
故答案为100,5.
(2)足球=100-30-20-10-5=35人,
条形图如图所示,
(3)若全校共有2000名学生,该校约有2000×$\frac{20}{100}$=400名学生喜爱打乒乓球.
(4)画树状图得:
∵一共有12种可能出现的结果,它们都是等可能的,符合条件的有两种,
∴P(B、C两人进行比赛)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.同时考查了概率公式.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F. 某电脑公司现有A、B、C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
某电脑公司现有A、B、C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
 如图,在△ABC中,∠A>∠B.
如图,在△ABC中,∠A>∠B. 如图,是二次函数y=ax2+bx+c的图象,对下列结论:①ab>0,②abc>0,③$\frac{4ac}{{b}^{2}}$<1,其中错误的个数是( )
如图,是二次函数y=ax2+bx+c的图象,对下列结论:①ab>0,②abc>0,③$\frac{4ac}{{b}^{2}}$<1,其中错误的个数是( )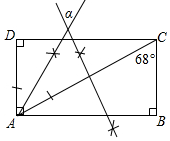 如图,依据尺规作图的痕迹,计算∠α=56°.
如图,依据尺规作图的痕迹,计算∠α=56°.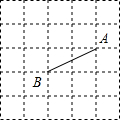 如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.
如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.