题目内容
11.已知点P是反比例函数y=$\frac{k}{x}$图象上一点,点P到原点O的距离OP=2,且OP与x轴正方向的夹角为120°,则k=±$\sqrt{3}$.分析 根据题意画出图形,进而结合勾股定理以及直角三角形的性质得出P,P′点坐标,进而得出答案.
解答  解:如图所示:过点P作PA⊥y轴于点A,过点P′作P′B⊥y轴于点B,
解:如图所示:过点P作PA⊥y轴于点A,过点P′作P′B⊥y轴于点B,
由题意可得:∠POA=∠P′OB=30°,
PO=P′O=2,
则PA=BP′=1,
故AO=OB=$\sqrt{3}$,
则P(-1,$\sqrt{3}$),P′(-1,-$\sqrt{3}$),
故k=±$\sqrt{3}$.
故答案为:±$\sqrt{3}$.
点评 此题主要考查了反比例函数图象上点的性质,得出P,P′点位置是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列各组数据中,结果相等的是( )
| A. | (-1)4与-14 | B. | -|-3|与-(-3) | C. | ${\frac{2}{3}^2}与{({\frac{2}{3}})^2}$ | D. | ${({\frac{-1}{3}})^3}与\frac{-1}{3^3}$ |
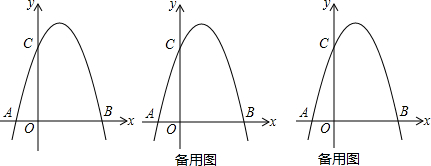
6.已知b>0时,二次函数y=ax2+bx+a2-4的图象如下列四个图之一所示,根据图象分析,a的值等于( )


| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
3.下列说法错误的是( )
| A. | 0是单项式 | |
| B. | 多项式2x3-3x+1是三次三项式 | |
| C. | 两个三次多项式相加得到的多项式是六次多项式 | |
| D. | $\frac{πx}{3}$的系数是$\frac{π}{3}$ |