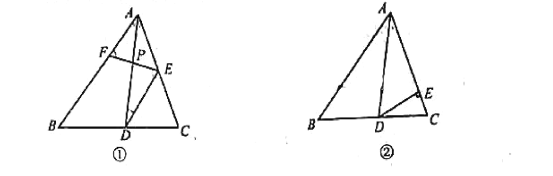题目内容
【题目】我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．
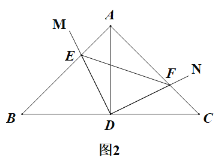
（1）如图①，在菱形ABCD中，∠ABC=120°，点M，N分别在AD，CD上，且∠MBN=60°，试判断四边形DMBN是否为“等邻边四边形”？请说明理由．
（2）如图②，在矩形ABCD中，AB=8，BC=12.5，点E在BC上，且BE=6，在矩形ABCD内或边上，确定一点P，使四边形ABEP为最大面积的“等邻边四边形”，若能实现，请求出最大面积；若不能实现，说明理由．
【答案】（1）是，理由见解析；（2）能实现，最大面积为
．理由见解析．
【解析】
（1）根据题意连接BD，则有结论即四边形DMBN是“等邻边四边形”，只要证明△MBD≌△NBC即可解决问题；
（2）根据题意分以A为圆心，AB为半径画弧，当点P在
（不包括点I）上时和以E为圆心，EB为半径画弧，当点P在
（不包括点H和点T）上时以及当点P在线段AE的垂直平分线上时三种情况进行讨论分析求解.
解：（1）结论：四边形DMBN是“等邻边四边形“．
理由：如图，连接BD，
∵四边形ABCD是菱形，∠ABC=120°，
∴∠ABD=∠CBD=60°，AB=BC=CD=AD，
∴△ABD，△BCD都是等边三角形，
∴BD=DC，∠MDB=∠C=60°，
∵∠MBN=∠DBC=60°，
∴∠MBD=∠NBC，
∴△MBD≌△NBC，
∴MB=BN，
∴四边形DMBN是“等邻边四边形“．
（2）能实现．
理由：如图，
以A为圆心，AB为半径画弧，
当点P在（不包括点I）上时，四边形ABEP是“等邻边四边形“，
点P在AD上时，当AB=AP时，四边形ABEP的面积的最大值为：
;
以E为圆心，EB为半径画弧，
当点P在（不包括点H和点T）上时，四边形ABEP是“等邻边四边形“，
有P′E⊥AE，AE=
，P′E=BE=6,四边形ABEP的面积的最大值为：
，
当点P在线段AE的垂直平分线上时，即AP=PE,易知AP=
，
此时四边形ABEP是“等邻边四边形“，面积=
．
综上所述，等邻边四边形ABEP的面积的最大值为：．
