题目内容
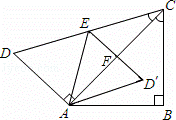
如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点.若AB=6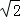 cm.
cm.
(1)AE的长为 4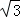 cm;
cm;
(2)试在线段AC上 确定一点P,使得DP+EP的值最小,并求出这个最小值;
确定一点P,使得DP+EP的值最小,并求出这个最小值;
(3)求点D′ 到BC的距离.
到BC的距离.
解:(1)∵∠BAC=45°,∠B=90°,
∴AB=BC=6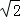 cm,
cm,
∴AC=12cm,
∵∠ACD=30°,∠DAC=90°,AC=12cm,
∴CD=AC÷cos30°=12÷ =12×
=12× =8
=8 (cm),
(cm),
∵点E为CD边上的中点,
∴AE= DC=4
DC=4 cm.
cm.
故答案为:4 ;
;
(2)∵Rt△ADC中,∠ACD=30°,
∴∠ADC=60°,
∵E为CD边上的中点,
∴DE=AE,
∴△ADE为等边三角形,
∵将△ADE沿AE所在直线翻折得△AD′E,
∴△AD′E为等边三角形,
∠AED′=60°,
∵∠EAC=∠DAC﹣∠EAD=30°,
∴∠EFA=90°,
即AC所在的直线垂直平分线段ED′,
∴点E,D′关于直线AC对称,
连接DD′交AC于点P,
∴此时DP+EP值为最小,且DP+EP=DD′,
∵△ADE是等边三角形,AD=AE=4 ,
,
∴DD′=2× AD×
AD× =2×6=12,
=2×6=12,
即DP+EP最小值为12cm;
(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,
∵AC垂直平分线ED′,
∴AE=AD′,CE=CD′,
∵AE=EC,∴AD′=CD′=4 ,
,
在△ABD′和△CBD′中,
 ,
,
∴△ABD′≌△CBD′(SSS),
∴∠D′BG=45°,
∴D′G=GB,
设D′G长为xcm,则CG长为(6 ﹣x)cm,
﹣x)cm,
在Rt△GD′C中
x2+(6 ﹣x)2=(4
﹣x)2=(4 )2,
)2,
解得:x1=3 ﹣
﹣ ,x2=3
,x2=3 +
+ (不合题意舍去),
(不合题意舍去),
∴点D′到BC边的距离为(3 ﹣
﹣ )cm.
)cm.


 某地为了打造风光带,将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24m,乙工程队每天整治16m.求甲、乙两个工程队分别整治了多长的河道.
某地为了打造风光带,将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24m,乙工程队每天整治16m.求甲、乙两个工程队分别整治了多长的河道.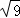 =
= 
 义务教育保障资金约为87 900 000 000元,请将数87 900 000 000用科学记数法表示为
义务教育保障资金约为87 900 000 000元,请将数87 900 000 000用科学记数法表示为  |﹣
|﹣ +(π+4)0﹣sin30°+
+(π+4)0﹣sin30°+ ;
;