题目内容
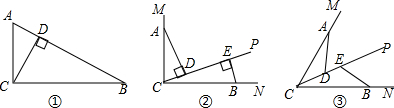
3.探究:如图①,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠B=30°,则∠ACD的度数是30度;拓展:如图②,∠MCN=90°,射线CP在∠MCN的内部,点A、B分别在CM、CN上,分别过点A、B作AD⊥CP、BE⊥CP,垂足分别为D、E,若∠CBE=70°,求∠CAD的度数;
应用:如图③,点A、B分别在∠MCN的边CM、CN上,射线CP在∠MCN的内部,点D、E在射线CP上,连接AD、BE,若∠ADP=∠BEP=60°,则∠CAD+∠CBE+∠ACB=120度.
分析 (1)利用直角三角形的性质依次求出∠A,∠ACD即可;
(2)利用直角三角形的性质直接计算得出即可;
(3)利用三角形的外角的性质得出结论,直接转化即可得出结论.
解答 解:(1)在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=90°-∠A=30°;
故答案为:30,
(2)∵BE⊥CP,
∴∠BEC=90°,
∵∠CBE=70°,
∴∠BCE=90°-∠CBE=20°,
∵∠ACB=90°,
∴∠ACD=90°-∠BCE=70°,
∵AD⊥CP,
∴∠CAD=90°-∠ACD=20°;
(3)∵∠ADP是△ACD的外角,
∴∠ADP=∠ACD+∠CAD=60°,
同理,∠BEP=∠BCE+∠CBE=60°,
∴∠CAD+∠CBE+∠ACB=∠CAD+∠CBE+∠ACD+∠BCE=(∠CAD+∠ACD)+(∠CBE+∠BCE)=120°,
故答案为120.
点评 此题是三角形的综合题,主要考查了直角三角形的性质,三角形的外角的性质,垂直的定义,解本题的关键是充分利用直角三角形的性质:两锐角互余,是一道比较简单的综合题.

练习册系列答案
相关题目
1.在△ABC中,∠C=90°,AC=3,BC=4,则tanA的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
2.在直角坐标系中,若一点的横坐标互为倒数,则该点一定在( )
| A. | y=-x | B. | y=x2 | C. | y=x | D. | y=$\frac{1}{x}$ |
11.下列各式正确的是( )
| A. | 0>-(-1)>-$\frac{2}{3}$>-|-$\frac{4}{5}$| | B. | -(-1)>0>-|-$\frac{4}{5}$|>-$\frac{2}{3}$ | C. | 0>-$\frac{2}{3}$>-|-$\frac{4}{5}$|>-(-1) | D. | -(-1)>0>-$\frac{2}{3}$>-|-$\frac{4}{5}$| |
18. 如图,△ABC≌△BAD,AC与BD是对应边,AC=8cm,AD=10cm,DE=CE=2cm,那么AE的长是( )
如图,△ABC≌△BAD,AC与BD是对应边,AC=8cm,AD=10cm,DE=CE=2cm,那么AE的长是( )
 如图,△ABC≌△BAD,AC与BD是对应边,AC=8cm,AD=10cm,DE=CE=2cm,那么AE的长是( )
如图,△ABC≌△BAD,AC与BD是对应边,AC=8cm,AD=10cm,DE=CE=2cm,那么AE的长是( )| A. | 8cm | B. | 10cm | C. | 2cm | D. | 不能确定 |
8.一个数a在数轴上的对应点在原点左边,且|a|=9,则a的值为( )
| A. | 9或-9 | B. | 9 | C. | -9 | D. | 以上都不对 |
15.下列方程中,关于x的一元二次方程是( )
| A. | (x+1)2=2(x+1) | B. | $\frac{1}{x^2}+\frac{1}{x}-2=0$ | C. | ax2+bx+c=0 | D. | x2+2x+c=x2-1 |
12.⊙O的半径为10cm,点A到圆心O的距离OA=8cm,则点A与⊙O的位置关系为( )
| A. | 点A在圆上 | B. | 点A在圆内 | C. | 点A在圆外 | D. | 无法确定 |
13.如果一个数的绝对值是它的相反数,则这个数是( )
| A. | 正数 | B. | 负数 | C. | 正数或零 | D. | 负数或零 |