题目内容
20.用“+”或“-”填空:(1)$\frac{b}{-3a}$=-$\frac{b}{3a}$;(2)$\frac{-a-b}{y-x}$=+$\frac{a+b}{x-y}$.
分析 (1)根据分式的分子、分母及分式的符号,只有同时改变两个其值才不变,可得答案;
(2)根据分式的分子、分母及分式的符号,只有同时改变两个其值才不变,可得答案.
解答 解:(1)改变分母、分式的符号,得
$\frac{b}{-3a}$=-$\frac{b}{3a}$;
(2)改变分子、分母的符号,得
$\frac{-a-b}{y-x}$=+$\frac{a+b}{x-y}$;
故答案为:-,+.
点评 本题考查了分式的基本性质,分式的分子、分母及分式的符号,只有同时改变两个其值才不变.

练习册系列答案
相关题目
15.股民李叔叔上星期五买进某公司1000股票,每股67元,下表为本周内每曰该股票收盘价的涨跌情况(单位:元),其中涨记正,跌记负.
(1)星期三收盘时,每股是多少元?
(2)本周内最高收盘价是每股多少元?最低收盘价为每股多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
(2)本周内最高收盘价是每股多少元?最低收盘价为每股多少元?
 如图,在△ABC中,BC=5cm,边长为2cm的正方形DEFG的一边EF在BC上,点D在AB上,点G在AC上,求△ABC的面积.
如图,在△ABC中,BC=5cm,边长为2cm的正方形DEFG的一边EF在BC上,点D在AB上,点G在AC上,求△ABC的面积.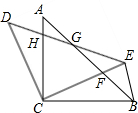 如图,在△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C按逆时针方向旋转一定角度,得到△DEC,连接BE.CE交于点F,DE分别交AB,AC于点G,H.
如图,在△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C按逆时针方向旋转一定角度,得到△DEC,连接BE.CE交于点F,DE分别交AB,AC于点G,H.