题目内容
9.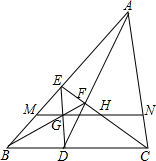 如图所示,已知D,E分别是△ABC的边BC,AB上的点,AD,CE交F,BF,DE交于G,过G作BC的平行线MN,交AB,CE,AC于M,H,N,求证:GH=NH.
如图所示,已知D,E分别是△ABC的边BC,AB上的点,AD,CE交F,BF,DE交于G,过G作BC的平行线MN,交AB,CE,AC于M,H,N,求证:GH=NH.
分析 过点E作ES∥BC,交AC于点S,根据平行线分线段成比例定理得到$\frac{CS}{SA}=\frac{BE}{EA}$、$\frac{FG}{GB}=\frac{FH}{HC}$,然后由梅捏劳斯定理得到$\frac{AD}{DF}•\frac{FG}{GB}•\frac{BE}{EA}=1$,从而得到$\frac{GH}{CD}=\frac{EG}{ED}=\frac{SN}{SC}=\frac{HN}{CD}$,最后证得GH=HN.
解答 解:过点E作ES∥BC,交AC于点S,
∴$\frac{CS}{SA}=\frac{BE}{EA}$,
∵NM∥BC,
∴$\frac{FG}{GB}=\frac{FH}{HC}$,
对于△ABF及截线EGD,由梅捏劳斯定理可得:
$\frac{AD}{DF}•\frac{FG}{GB}•\frac{BE}{EA}=1$,
∴$\frac{AD}{DF}•\frac{FH}{HC}•\frac{CS}{SA}=1$,
由梅捏劳斯定理可知:S、H、D共线,
∴$\frac{GH}{CD}=\frac{EG}{ED}=\frac{SN}{SC}=\frac{HN}{CD}$,
∴GH=HN.
点评 本题考查了梅涅劳斯定理的知识,解题的关键是了解梅捏劳斯定理的内容,综合性较强,难度较大.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
4.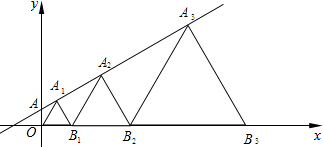 如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
 如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )| A. | ($\frac{\sqrt{3}}{3}$)9 | B. | ($\frac{\sqrt{3}}{3}$)10 | C. | 29•$\sqrt{3}$ | D. | 210•$\sqrt{3}$ |
19.下列不等式变形正确的是( )
| A. | 由a>b,得a-2<b-2 | B. | 由a>b,得a2>b2 | C. | 由a>b,得|a|>|b| | D. | 由a>b,得-2a<-2b |
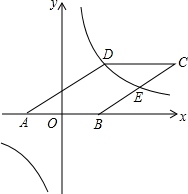 如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D.点P是该反比例函数图象上的一个动点,且点P在该反比例函数图象上的第一象限内,当S△PAB=S△ODE时(两三角形面积相等),求点P的坐标.
如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D.点P是该反比例函数图象上的一个动点,且点P在该反比例函数图象上的第一象限内,当S△PAB=S△ODE时(两三角形面积相等),求点P的坐标.
 已知四个数:a=(-2)2,b=-(-2),c=(-1)2013,d=-|-3|.
已知四个数:a=(-2)2,b=-(-2),c=(-1)2013,d=-|-3|.