题目内容
11.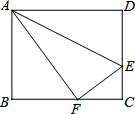 折叠长方形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长是5$\sqrt{5}$cm.
折叠长方形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长是5$\sqrt{5}$cm.
分析 首先根据勾股定理求出BF的长度,进而求出CF的长度;再根据勾股定理求出EF的长度问题即可解决.
解答 解:由题意得:AF=AD,EF=DE,
∵四边形ABCD为矩形,
∴AF=AD=BC=10,DC=AB=8;∠ABF=90°;
由勾股定理得:BF2=102-82=36,
∴BF=6,CF=10-6=4;
在直角三角形EFC中,设EF=DE=x,
由勾股定理得:x2=42+(8-x)2,
解得:x=5,
∴AE2=102+52=125,
∴AE=5$\sqrt{5}$(cm).
故答案为:5$\sqrt{5}$cm.
点评 此题考查了翻折变换及勾股定理的运用,图形对折的问题一定要注意,折叠前的图形与折叠后的图形全等.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
16.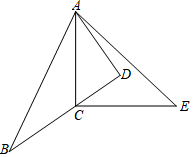 一副三角板如图放置,则下列说法中正确的有( )
一副三角板如图放置,则下列说法中正确的有( )
①∠CAD+∠BAE等于定值105°
②若BD过点C,则一定有AB⊥AE;
③若BD过点C,则一定有∠DAE+∠DCE=45°.
 一副三角板如图放置,则下列说法中正确的有( )
一副三角板如图放置,则下列说法中正确的有( )①∠CAD+∠BAE等于定值105°
②若BD过点C,则一定有AB⊥AE;
③若BD过点C,则一定有∠DAE+∠DCE=45°.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.当代数式x2+3x+5的值为7时,代数式3x2+9x-2的值为( )
| A. | 4 | B. | 2 | C. | -2 | D. | -4 |
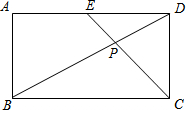 学完第七章《平面直角坐标系》和第十九章《一次函数》后,老师布置了这样一道思考题:已知:如图,在长方形ABCD中,BC=4,AB=2,点E为AD的中点,BD和CE相交于点P.求△BPC的面积.
学完第七章《平面直角坐标系》和第十九章《一次函数》后,老师布置了这样一道思考题:已知:如图,在长方形ABCD中,BC=4,AB=2,点E为AD的中点,BD和CE相交于点P.求△BPC的面积.


