题目内容
13.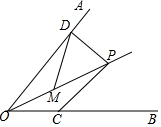 如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 1cm |
分析 根据角平分线的定义可得∠AOP=$\frac{1}{2}$AOB=30°,再根据直角三角形的性质求得PD=$\frac{1}{2}$OP=4,然后根据角平分线的性质和垂线段最短得到结果.
解答 解:∵P是∠AOB角平分线上的一点,∠AOB=60°,
∴∠AOP=$\frac{1}{2}$AOB=30°,
∵PD⊥OA,M是OP的中点,DM=4cm,
∴OP=2DM=8,
∴PD=$\frac{1}{2}$OP=4,
∵点C是OB上一个动点,
∴PC的最小值为P到OB距离,
∴PC的最小值=PD=4.
故选C.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形的性质,熟记性质并作出辅助线构造成直角三角形是解题的关键.

练习册系列答案
相关题目
4.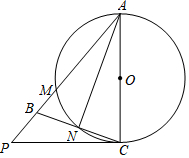 如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
(1)求证:∠BCD=∠BAN.
(2)若AC=4,PC=3,求MN•BC的值.
 如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.(1)求证:∠BCD=∠BAN.
(2)若AC=4,PC=3,求MN•BC的值.
8.下列计算正确的是( )
| A. | (3xy2)2=6xy4 | B. | a+2a2=3a3 | C. | (-x)7÷(-x)2=-x5 | D. | 3x2+4x2=7x4 |
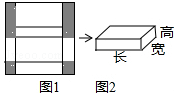 图1是边长为30的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知长方体的宽是高的2倍,求该长方体盒子的体积和表面积.
图1是边长为30的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知长方体的宽是高的2倍,求该长方体盒子的体积和表面积.