题目内容
9．（1）解二元一次方程组$\left\{\begin{array}{l}{2x+3y=15}\\{3x+5y=30}\end{array}\right.$（2）画出不等式组$-2≤\frac{3}{x+1}＜5$在数轴上的解集．
分析 （1）方程组利用加减消元法求出解即可；
（2）求出不等式组的解集，表示在数轴上即可．
解答 解：（1）$\left\{\begin{array}{l}{2x+3y=15①}\\{3x+5y=30②}\end{array}\right.$，
①×5-②×3得：x=-15，
把x=-15代入①得：y=15，
则方程组的解为$\left\{\begin{array}{l}{x=-15}\\{y=15}\end{array}\right.$；
（2）不等式组整理得：$\left\{\begin{array}{l}{-2x-2≤3①}\\{5x+5＞3②}\end{array}\right.$，
由①得：x≥-$\frac{5}{2}$；
由②得：x＞-$\frac{2}{5}$，
∴不等式组的解集为x＞-$\frac{2}{5}$，
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
教材全解字词句篇系列答案
相关题目
20．
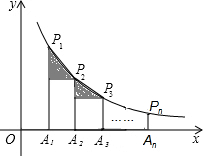如图，在x轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An（n为正整数），过点A1、A2、A3、…、An分别作x轴的垂线，与反比例函数y=$\frac{2}{x}$（x＞0）交于点P1、P2、P3、…、Pn，连接P1P2、P2P3、…、Pn-1Pn，过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段，构成的一系列直角三角形（见图中阴影部分）的面积和是（ ）
如图，在x轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An（n为正整数），过点A1、A2、A3、…、An分别作x轴的垂线，与反比例函数y=$\frac{2}{x}$（x＞0）交于点P1、P2、P3、…、Pn，连接P1P2、P2P3、…、Pn-1Pn，过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段，构成的一系列直角三角形（见图中阴影部分）的面积和是（ ）| A． | $\frac{n-1}{n}$ | B． | $\frac{n}{n+1}$ | C． | $\frac{1}{{2}^{n}}$ | D． | $\frac{1}{{4}^{n}}$ |
17．在一次中学生田径运动会上，参加跳高的15名运动员的成绩如表：那么这些运动员跳高成绩的众数和中位数分别是（ ）
| 成绩（m） | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
| A． | 4和1.60 | B． | 1.75和1.65 | C． | 1.65和1.675 | D． | 1.65和1.70 |
4．某中学2012年投资11万元新增一批电脑，计划以后每年以相同的增长率进行投资，2014年投资18.59万元．则该学校为新增电脑投资的年平均增长率为（ ）
| A． | 18% | B． | 15% | C． | 28% | D． | 30% |
14．将一枚质地均匀的硬币抛掷两次，则两次都是正面向上的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{4}$ |
如图，在菱形ABCD中，cosA=$\frac{3}{5}$，BE=2，则tan∠BDE=2．