题目内容
10.小明开了一家网店,进行社会实践,计划经销甲、乙两种商品.若甲商品每件利润20元,乙商品每件利润10元,则每周能卖出甲商品120件,乙商品40件.经调查,甲、乙两种商品零售单价分别每降价1元,这两种商品每周可多销售10件.为了提高销售量,小明决定把甲、乙两种商品的零售单价都降价x元.(1)直接写出甲、乙两种商品每周的销售量y(件)与降价x(元)之间的函数关系:y甲=120+10x,y乙=40+10x;
(2)求出小明每周销售甲、乙两种商品获得的总利润W(元)与降价x(元)之间的函数关系式?如果每周乙商品的销售量不低于甲商品的销售量的$\frac{5}{3}$,那么当x定位多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
分析 (1)根据题意可以列出甲、乙两种商品每周的销售量y(件)与降价x(元)之间的函数关系式;
(2)根据每周甲商品的销售量不低于乙商品的销售量的$\frac{3}{2}$,列出不等式求出x的取值范围,根据题意列出二次函数的解析式,根据二次函数的性质求出对称轴方程,得到答案.
解答 解:(1)由题意得,y甲=10x+120;
y乙=10x+40;
(2)由题意得,
W=(20-x)(10x+120)+(10-x)(10x+40)
=-20x2+140x+2800,
由题意得,$\frac{5}{3}$(10x+40)≤10x+120
解得x≤$\frac{16}{5}$,
W=-20x2+140x+2800
=-20(x-$\frac{7}{2}$)2+3520,
∵a=-20<0,
∴当x≤$\frac{16}{5}$时,W随x增大而增大,
∴当x=$\frac{16}{5}$时,W的值最大.
答:当x定为6元时,才能使小明每周销售甲、乙两种商品获得的总利润最大.
点评 本题考查的是二次函数的应用,正确列出二次函数的关系式,掌握二次函数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.根据近三年的统计显示,新昌大佛寺旅游景点的旅游人次呈逐年增长趋势,预计2016年能达到9690000人次,将9690000用科学记数法表示为( )
| A. | 0.969×107 | B. | 9.69×107 | C. | 9.69×106 | D. | 969×104 |
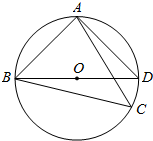 如图,点C为△ABD的外接圆上的一动点(点C不在$\widehat{BAD}$上,且不与点B,D重合),∠ACB=∠ABD=45°
如图,点C为△ABD的外接圆上的一动点(点C不在$\widehat{BAD}$上,且不与点B,D重合),∠ACB=∠ABD=45° 如图,在?ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.
如图,在?ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE. 如图,在平行四边形ABCD中,AB=4,BC=8,∠B=60°,过平行四边形的对称中心点O的一条直线与边AD、BC分别交于点E、F,设直线EF与BC的夹角为α(如图)
如图,在平行四边形ABCD中,AB=4,BC=8,∠B=60°,过平行四边形的对称中心点O的一条直线与边AD、BC分别交于点E、F,设直线EF与BC的夹角为α(如图) 如图,河坝横断面背水坡AB的坡角是45°,背水坡AB长度为20$\sqrt{2}$米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】
如图,河坝横断面背水坡AB的坡角是45°,背水坡AB长度为20$\sqrt{2}$米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】