题目内容

11．点A（x1，y1）、B（x2、y2）、C（x3、y3）是反比例函数y=$\frac{{k}^{2}+5}{x}$的图象上三点，且x1＜x2＜0＜x3，用“＜”将函数值y1、y2、y3连接起来y2＜y1＜y3．

分析 根据反比例函数y=$\frac{{k}^{2}+5}{x}$的比例系数k2+5＞0，判断出函数图象在一、三象限，在每个象限内，y随x的增大而减小，再根据x1＜x2＜0＜x3，判断出y1、y2、y3的大小．

解答 解：∵反比例函数y=$\frac{{k}^{2}+5}{x}$的比例系数k2+5＞0，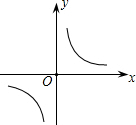
∴该反比例函数的图象如图所示，该图象在第一、三象限，在每个象限内，y随x的增大而减小，
又∵x1＜x2＜0＜x3，
∴y2＜y1＜y3．
故答案为y2＜y1＜y3．

点评 本题考查了反比例函数图象上点的坐标特征．注意是在每个象限内，y随x的增大而减小．不能直接根据x的大小关系确定y的大小关系．

练习册系列答案
相关题目
1．下列式子不是二次根式的是（　　）
A．$\sqrt{5}$B．$\sqrt{{a^2}+1}$C．$\sqrt{1.2}$D．$\sqrt{-|x|-1}$
2．观察下列等式
$\frac{1}{1×2}=1-\frac{1}{2}$，$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$，$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$，
将以上三个等式两边分别相加得：
$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}$=1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$．
（1）猜想并写出：$\frac{1}{n（n+1）}$$\frac{1}{n}$-$\frac{1}{n+1}$．
（2）根据以上规律直接写出下列各式的计算结果：$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$=$\frac{2014}{2015}$；
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n（n+1）}$$\frac{n}{n+1}$．
（3）探究并计算：$\frac{1}{2×4}+\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2012×2014}$．
19．在有理数：-2，-（-2），|-2|，-|+2|，-|-2|，+（-2），-（+2）中负数有（　　）
A．6个B．5个C．4个D．3个
6．在平面直角坐标系中，抛物线y=x2-x-6的图象向左平移m（m＞0）个单位后过原点，则m的值为（　　）
A．1B．2C．3D．6
16．已知抛物线y=ax2+bx+c经过A（-3，0）、B（2，5），C（0，-3）三点．
（1）求抛物线的解析式；
（2）若ax2+bx+c＞0，直接写出x的取值范围是x＜-3或x＞1．
3．解方程：
①x2-4x-45=0
②（2x+1）2=3（2x+1）
20．（$\root{3}{-8}$）3=-8；${（{\root{3}{-27}}）^3}$=-27．
1．飞机着陆后滑行的距离S（单位：m）关于滑行时间t（单位：s）的函数解析式是：S=60t-1.5t2
（1）直接指出飞机着陆时的速度；
（2）直接指出t的取值范围；
（3）画出函数S的图象并指出飞机着陆后滑行多远才能停下来？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网