题目内容
已知一个二次函数的图象是由抛物线y=
x2上下平移得到的,且当x=-1时,y=
.
(1)求此二次函数解析式;
(2)当x为何值时,y随着x的增大而减小.
| 3 |
| 2 |
| 5 |
| 2 |
(1)求此二次函数解析式;
(2)当x为何值时,y随着x的增大而减小.
考点:二次函数图象与几何变换
专题:
分析:(1)根据上下平移设二次函数解析式为y=
x2+c,然后把x、y的值代入计算即可得解;
(2)根据二次函数的增减性解答.
| 3 |
| 2 |
(2)根据二次函数的增减性解答.
解答:解:(1)设二次函数解析式为y=
x2+c,
∵x=-1时,y=
,
∴
×(-1)2+c=
,
解得c=1.
所以y=
x2+1;
(2)∵a=
>0,
∴x<0时,y随着x的增大而减小.
| 3 |
| 2 |
∵x=-1时,y=
| 5 |
| 2 |
∴
| 3 |
| 2 |
| 5 |
| 2 |
解得c=1.
所以y=
| 3 |
| 2 |
(2)∵a=
| 3 |
| 2 |
∴x<0时,y随着x的增大而减小.
点评:本题考查了二次函数图象与几何变换,二次函数图象上点的坐标特征,二次函数的增减性,熟记性质是解题的关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
有一种细菌的半径是0.00000026微米,用科学记数法表示为( )
| A、2.6×10-6元 |
| B、2.6×10-7元 |
| C、-2.6×10-6元 |
| D、2.6×10-8元 |
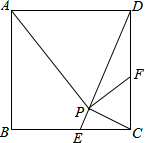 如图,在正方形ABCD中,已知CE=CF,CP⊥DE于点P,求证:PA⊥PF.
如图,在正方形ABCD中,已知CE=CF,CP⊥DE于点P,求证:PA⊥PF. 图(1)是图(2)正方体的表面展开图,请在图(2)的正方体中将线段BD、EF画出来.
图(1)是图(2)正方体的表面展开图,请在图(2)的正方体中将线段BD、EF画出来. 如图,已知PA、PB为⊙O的切线,切点分别为点A、B,∠P=60°,AB=4
如图,已知PA、PB为⊙O的切线,切点分别为点A、B,∠P=60°,AB=4 已知△ABC(如图),用直尺和圆规作△DEF,使△DEF≌△ABC.
已知△ABC(如图),用直尺和圆规作△DEF,使△DEF≌△ABC.